Разделы
Счетчики
4. Объекты 0-го и 1-го порядка
Интегральная теория создания ИИ
По сути дела объект 0-го порядка введен для придания нашим рассуждениям формальной полноты и означает отсутствие чего-либо. Математический аналог - пустое множество.
Объект 1-го порядка представляет собой какую-либо неоднородность, в результате чего его можно выделить на общем однородном фоне. В нашем мире объектами 1-го порядка являются различного рода физические неоднородности.
Так как при рассмотрении объекта 1-го порядка нам важен лишь факт его существования и принцип деления на отдельные элементы, а не природа его физического устройства и происхождения, то для его полного описания необходимо и достаточно переменной, представляющей из себя точку в многомерном пространстве: X(x1,x2,...,xn), где x1,x2,...,xn - координаты, относительно которых идет описание физической неоднородности.
Если объект 1-го порядка описывается n-мерной переменной, то его можно представить как совокупность более мелких объектов 1-го порядка, описываемых m1,m2,...,mi-мерными переменными, причем m1+m2+...+mi=n. Затем и эти объекты можно представить как совокупность еще более мелких объектов 1-го порядка. В результате в конце мы придем к объектам 1-го порядка, описываемым одномерной переменной. Можно пойти еще дальше и представить их в виде набора двоичных переменных (принимающих только 2 значения: 0 или 1). Эти объекты уже невозможно поделить, и поэтому мы назовем их математически элементарными объектами 1-го порядка. Необходимо отметить важное отличие математически элементарных объектов от физически элементарных. Физически элементарный объект 1-го порядка представляет собой лишенную сложной внутренней структуры физическую неоднородность. В противоположность математически элементарным объектам физически элементарный объект нельзя делить до двоичного теоретического предела, даже если он и описывается многомерной переменной, ввиду отсутствия множества составляющих его элементов.
Введем понятие числа состояний математически элементарного объекта 1-го порядка. Поскольку описывающая его одномерная переменная может принимать различные значения, то число состояний математически элементарного объекта 1-го порядка будет равно количеству этих значений. Совокупность таких значений образует множество возможных состояний объекта 1-го порядка. Каждый элемент этого множества - одно из возможных состояний объекта 1-го порядка. Множество может быть конечным (имеет конечное число элементов), счетным (число элементов равно числу натуральных чисел) или несчетным (число элементов равно числу дробных чисел на отрезке 0..1).
Сложность объекта 1-го порядка можно оценить мощностью множества (напомним, что мощностью множества называется число его элементов; чем больше это число, тем мощнее множество) всех его возможных состояний. Представим объект 1-го порядка X как совокупность математически элементарных объектов x1,x2,...,xn. И пусть, например, x1 может принимать k1 возможных состояний, x2 может принимать k2 состояний, ..., xn - kn состояний. Тогда X может принимать k1*k2*...*kn возможных состояний. Поэтому мы можем сказать, что объекту 1-го порядка сопоставляется одноименное множество X с мощностью |X|=k1*k2*...*kn. Введя одноименное множество состояний для каждого математически элементарного объекта x1,x2,...,xn, мы можем записать мощность множества X как произведение мощностей множеств x1,x2,...,xn: |X|=|x1|*|x2|*...*|xn|. Этой формой записи мы и будем пользоваться в дальнейшем. Величину |X| станем называть уровнем объекта 1-го порядка.
Из сказанного очевидно, что физически неэлементарный объект 1-го порядка можно представить в виде совокупности двух и более объектов 1-го порядка. Справедливо и обратное: любой объект 1-го порядка может быть частью другого, более крупного объекта 1-го порядка.
Какие условия необходимы для существования объектов 1-го порядка? Так как объект 1-го порядка - это физическая неоднородность, то следовательно для его существования необходимо и достаточно, чтобы та часть Мира, в которой он находится - его среда функционирования - была анизотропной. Графически объект 1-го порядка будем представлять в виде прямоугольника с одинарной линией, и названием этого объекта внутри него, например:
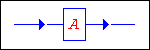
Очевидно, что модификаций у объекта 1-го порядка всего одна. Эти объекты различаются только своим уровнем, отсюда и краткое обозначение объекта 1-го порядка - объект класса 1.1. Объект 1-го порядка - это физический способ записи переменной - абстрактного математического понятия.
Атомы, молекулы... Все то, характеристики чего можно описать многомерной переменной - объект 1-го порядка. Все наблюдаемые нами объекты 1-го порядка с точки зрения современной науки имеют сложную внутреннюю структуру, а значит не являются физически элементарными. В повседневной жизни (и в частности в программировании) при помощи объектов 1-го порядка хранятся данные. Однако нельзя в общем виде приписывать объект 1-го порядка каким-нибудь там значениям ячеек в памяти компьютера. Объектом 1-го порядка может быть любая неоднородность - расположение звезд на небе, смена дня и ночи, шум падающей воды и так далее.
newpoisk.narod.ru, 21 марта 2005 года