5. Объекты 2-го порядка

Интегральная теория создания ИИ

Итак, объект 1-го порядка - это физическая неоднородность, описываемая через многомерную переменную. Но есть и такие объекты, которые нельзя описать с помощью одних только переменных, где существует зависимость состояния одних объектов 1-го порядка от состояния других объектов 1-го порядка. Но раз есть зависимость, то в общем виде она может стать эквивалентной управлению. Так мы приходим к объекту 2-го порядка.

Объект 2-го порядка есть процесс преобразования объектов 1-го порядка. Поскольку состояние объекта 1-го порядка описывается многомерной переменной, то зависимость состояния одного объекта 1-го порядка от другого можно описать в виде функции - зависимости значения одной многомерной переменной от другой: B=f(A), где A - переменная, описывающая исходный объект 1-го порядка, В - зависимый объект 1-го порядка, f - функция зависимости.

В общем случае зависимость B=f(A) может носить произвольный характер: функция f может быть логической (IF...THEN...ELSE), аналитической и прочей. В самом общем виде функция f - это отображение множества состояний A на множество состояний B. Каждой совокупности состояний A сопоставляется соответствующая совокупность (или совокупности в случае так называемого неопределенного объекта 2-го порядка) состояний B. С учетом возможности разложения объектов A и B на математически элементарные составляющие A=(a₁,a₂,...,a_n), B=(b₁,b₂,...,b_m) очевидно, что функция f представима в виде нескольких функций, отражающих зависимость элементарных объектов: f=(f₁,f₂,...,f_m), где b₁=f₁(...,a_i,....), b₂=f₂(...,a_j,....), и так далее. Уровень объектов A и B: p=|A| и q=|B| может быть любым.

В дальнейшем мы будем также рассматривать так называемый интерпретатор - механизм, реализующий функцию f. Не следует смешивать понятия интерпретатора и функции зависимости. Интерпретатор - это реально существующий физический механизм, в то время как функция - лишь описание его проявления на объектах 1-го порядка. Обозначать интерпретатор будем через букву I: например B=I(A).

Из теории объектов (а именно из существования фундаментальных свойств в объектах более высокого порядка относительно объектов более низкого порядка) следует, что круг необходимых и достаточных свойств среды функционирования объектов порядка N расширится при переходе к объектам порядка N+1. И если для объектов 1-го порядка среда функционирования должна была обладать анизотропностью, то для существования объектов 2-го порядка нужно что-то еще. Что они должны собой представлять? По всей видимости, в результате их введения должна появиться возможность создавать интерпретатор. Интерпретатор у нас состоит из 2-х частей: физической - собственно механизм преобразования, и логической - функции, описывающей процесс преобразования. Отсюда следует, что должно появиться 2 новых требования к среде функционирования: 1) между объектами 1-го порядка А и В должно существовать взаимодействие; 2) это взаимодействие должно описываться неизменяющимися функциями f, то есть они не должны носить, например, случайный характер (взаимодействие существует, но описать его мы не в состоянии, поскольку любая функция строится по определенному алгоритму, а значит уже не случайна).

Существования взаимодействия между A и B в рамках объекта 2-го порядка означает возможность изменения свойств B в зависимости от состояния A. Последнее вызывает необходимость описывать свойства B через свойства A. Получается, что A и B должны обладать эквивалентными свойствами. Необходимость наличия эквивалентности A и B совсем не говорит о том, что все свойства рассматриваемых объектов 1-го порядка должны быть эквивалентными - вполне возможно, что они будут содержать и фундаментальные относительно друг друга свойства. Просто в этом случае наличие фундаментальных свойств в A и B не учитывается и они не фигурируют в функции B=f(A).

Рассмотрим случаи так называемых общих и синхронных осей. Если многомерные переменные, соответствующие объектам 1-го порядка A и B, имеют вид A(a₁,a₂,...,c,a_n,a_n+1,...) и A(b₁,b₂,...,c,b_n,b_n+1,...), то c - общая ось. Если значения A и B на оси c всегда равны, то ось c - синхронная ось. Так как значения объектов A и B на синхронной оси всегда равны, то она является неинформативной - ее всегда можно убрать из рассмотрения безо всякого ущерба.

Введем понятие принципа суперпозиции - когда на состояние каждого физически элементарного объекта 1-го порядка могут одновременно влиять 2 или более объекта 2-го порядка:

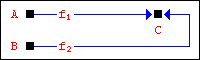
A, B, C - объекты 1-го порядка, f₁, f₂ - функции зависимости состояния C от A и B. C=g(f₁(A);f₂(B)). Функция g служит так называемым уравнением связи и определяет суперпозицию действия функций f₁ и f₂ на C, например C=g(f₁(A);f₂(B))=f₁(A)+f₂(B) или C=g(f₁(A);f₂(B))=f₁(A)·f₂(B).

Уравнение связи также является объектом 2-го порядка, но не совсем обычным. Оно показывает, какие свойства среды функционирования являются общими для некоторых объектов 2-го порядка. Например, в нашем мире уравнением связи служит операция "+". Суммарное воздействие на элементарную частицу электрических, магнитных, гравитационных и других полей от нескольких источников рассчитывается как их геометрическая сумма (как сумма соответствующих векторов).

Небольшое, но важное отступление: существование принципа суперпозиции не является неотъемлемым свойством системы из нескольких объектов 2-го порядка. Более того, сам факт существования какой-либо связи между работой нескольких объектов 2-го порядка выходит за пределы теории объектов 2-го порядка! Данное ограничение распространяется на все случаи совместного рассмотрения работы объектов 2-го порядка. Это может быть система из нескольких объектов 2-го порядка (наподобие объединения в систему отдельных уравнений). Возможно также, что в функции описания интерпретатора I(A) значения переменных a₁,a₂,...,a_n будут зависеть друг от друга, то есть опять возникает система уравнений вида a₁=a₁+a₂; a₂=a₅-a₁₀+a₃·a₁ и так далее.

Подробное рассмотрение явления взаимосвязи объектов 2-го порядка, приводящее к появлению эффектов, подобных принципу суперпозиции, будет подробно рассмотрено в теории объектов 3-го порядка (свойство универсального интерфейса). В текущей же главе указанная поправка несущественна. В ней, рассуждая о системах объектов 2-го порядка, мы будем подразумевать наличие принципа суперпозиции как нечто само собой разумеющееся.

Аналогично понятиям математически и физически элементарных объектов 1-го порядка введем понятия математически и физически элементарных объектов 2-го порядка.

Математически элементарный объект 2-го порядка. Как известно любая сложная функция разлагается на ряд простейших неделимых операций. Например, любой алгоритм - это набор всего лишь 3-х простейших операторов: присвоения, логического условия, производящего переход в определенное место алгоритма, и набора операций обработки данных, являющихся математическими операциями. Однако любая математическая операция (умножение, деление, возведение в степень и так далее) имеет в своей основе операцию сложения. Одним словом, для каждого вида зависимостей существует базовый набор элементарных компонентов. Следовательно, функция любого объекта 2-го порядка эквивалентна определенной совокупности своих элементарных компонентов - математически элементарных объектов 2-го порядка.

Физически элементарный объект 2-го порядка. В физической реальности, как правило, мы не имеем возможности дробить любой произвольный объект 2-го порядка на математически элементарные составляющие. На каком-то шаге явление зависимости между объектами 1-го порядка (тоже, как правило, неэлементарных) перестает быть набором способных к автономному физическому существованию компонентов. Мы получаем физически элементарный объект 2-го порядка. Математически он может быть неэлементарен. Существенно: участвующие в работе физически элементарного объекта 2-го порядка объекты 1-го необязательно физически элементарны.

Интерпретатор. Ядро объекта 2-го порядка, содержащее неописываемые многомерными переменными свойства. Каково его реальное внутреннее устройство? Вряд ли мы когда-нибудь дадим исчерпывающий ответ, сумеем только описать его при помощи некоей зависимости - функции f, построенной на элементарных операциях, также в свою очередь являющихся механизмами зависимости, хотя и более простыми. Например, функция B=10·A представима как B=A+A+A+A+A+A+A+A+A+A, а операция "+" и есть та самая элементарная операция - простейший неделимый далее механизм зависимости. Но для описания принципов работы объектов 2-го порядка, нам в общем-то и не нужно знать их реальное внутреннее устройство. Математического описания функции f вполне достаточно (ситуация аналогична той, что была при рассмотрении объектов 1-го порядка, когда при создании математической модели мы не учитывали его реальное устройство). Математическую модель интерпретатора (то есть функцию f, рассмотренную выше) следует рассматривать как функцию вида B=I(A), где A - входной объект 1-го порядка, B - выходной объект 1-го порядка. Причем A₁,A₂,...,A_q - возможные состояния объекта A, q=|A|. Причем также B₁,B₂,...,B_p - возможные состояния объекта B, p=|B|.

Существуют 2 разновидности объекта 2-го порядка: объект класса 2.1 и объект класса 2.2 (остальные схемы являются их сочетанием). Рассмотрим их подробнее.

newpoisk.narod.ru, 21 марта 2005 года