5.1. Объект класса 2.1

Интегральная теория создания ИИ

Объект класса 2.1 возникает, когда A=B, а зависимость принимает вид A=f(A). Графически объект класса 2.1 можно изобразить следующим образом:

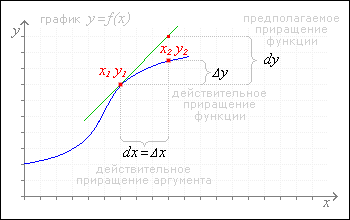
Символы "A" и "С" обозначают объекты 1-го порядка. Символ "I" обозначает интерпретатор объекта 2-го порядка - механизм, обеспечивающий изменение объекта 1-го порядка, стоящего у него на выходе, на основе информации, получаемой от объекта 1-го порядка, стоящего у него на входе.

Объект 1-го порядка C является вспомогательным и служит для построения функции A=I(A) (либо B=I(A) для случая объекта класса 2.2). Он может как существовать, так и отсутствовать. В общем случае ничего нельзя сказать ни о размерности пространства, в котором он существует, ни о |C|. Объект C является подсистемой интерпретатора и может быть невидим для стороннего наблюдателя. В принципе его можно рассматривать как совокупность промежуточных переменных алгоритма работы интерпретатора.

Причины, по которым происходят изменения объекта A, лежат за пределами теории объектов 2-го порядка и мы рассматривать их не будем.

Объект класса 2.1 описывается уравнением A=I(A). Решения этого уравнения (если они существуют) представляют собой набор определенных состояний объекта A. Таким образом, для внешнего наблюдателя этот случай можно в принципе свести к объекту 1-го порядка C, состоящего из набора решений. Приведем небольшой пример. Дано: A(a₁,a₂); I(A)=(a₁·a₁-a₁+1,a₂·a₂); a₁=(0,1,2,3,4,5); a₂=(0,1,2).

Найдем решения: нужно решить уравнение A=I(A). Для этого составим такую систему уравнений: a₁=a₁·a₁-a₁+1; a₂=a₂·a₂. Решив эту систему, найдем следующие корни: a₁=(1); a₂=(0,1). Таким образом, объект A может принимать 2 состояния: A(1,0); A(1,1). Следовательно, его можно без потери информативности для внешнего наблюдателя заменить объектом 1-го порядка C, принимающим 2 возможных состояния: C(1,0) и C(1,1).

Особо обращаем внимание читателя на то важное обстоятельство, что указанные уравнения не являются рекурсивными вида A(i)=f(A(i-1)), где A(i-1) - предыдущее состояние, A(i) - текущее состояние. То есть текущее состояние не является следствием предыдущего. Почему это так, смотрите пункт "Переходы решений".

Обобщением объектов класса 2.1 являются так называемые кольцевые структуры, устройство которых проиллюстрировано:

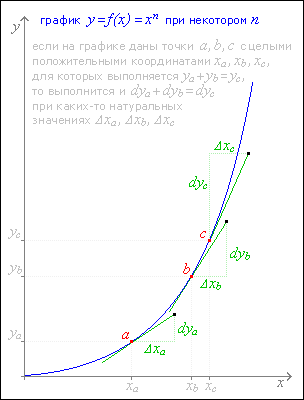
В пределе в кольцевой структуре реализуется максимально общий случай взаимодействия: состояние каждого объекта 1-го порядка находится в зависимости от любого другого входящего в кольцевую систему объекта 1-го порядка и от самого себя. При этом уровни объектов 1-го порядка могут быть неравными: |A|<>|B|<>|C|, а функции связи любого вида (логические, аналитические и тому подобные). В показанном на рисунке случае каждый объект имеет возможность непосредственного воздействия на другой объект, но возможны системы, в которых реализуется косвенное влияние. Более подробно теория кольцевых структур будет освещена в разделе "Принципы построения объектов 3-го порядка".

newpoisk.narod.ru, 21 марта 2005 года