5.4. Переходы решений. Системы объектов 2-го порядка

Интегральная теория создания ИИ

Под решениями объекта B=I(A) понимается набор значений (a₁, b₁), (a₂, b₂) и так далее, удовлетворяющих уравнению B=I(A). В случае объекта A=I(A) соответствующими решениями будут a₁,a₂,...,a_n, удовлетворяющие уравнению A=I(A). Напомним, что вид функций связи для объектов 2-го порядка может носить произвольную (аналитическую, логическую, либо другую) форму. Переход решений - явление изменения решения (a_i, b_j) на (a_k, b_l) для объекта класса 2.2 или a_i на a_j в случае объекта класса 2.1. То есть одно множество состояний объектов 1-го порядка, входящих в состав объекта 2-го порядка, уступает место другому.

Переход решений в физически элементарном объекте класса 2.2 B=I(A) происходит в результате изменений состояния объектов A и B. Сложнее дело обстоит в случае с 2.1: A=I(A). Первоначальный и наиболее важный вопрос, касающийся причин изменения состояния A: каков характер уравнения A=f(A) - оно обыкновенное или рекурсивное? Допустим, что рекурсивно. Тогда A(i)=I(A(i-1)), где A(i) - текущее состояние, A(i-1) - предыдущее (его можно рассматривать также как внутреннюю переменную интерпретатора). Рассмотрим пошагово режим работы интерпретатора в рекурсивном режиме:

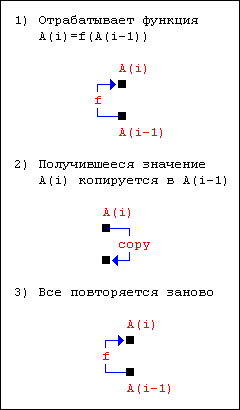
Очевидно, что в момент работы функции копирования текущего состояния в предыдущее (шаг 2, функция copy) функция f должна быть отключена. Равносильно и в момент работы f функция copy должна быть отключена. Выходит, что, например, f должна то существовать, то нет. А это противоречит 2-му требованию к среде существования объектов 2-го порядка, говорящему о том, что функциональные зависимости должны быть неизменными. Да и как определить, когда нужно "включать" f, а когда "отключать"? А поскольку мы рассматриваем объект A=I(A) в изолированном виде, то сторонних средств, обеспечивающих переключение управления между f и copy, не существует. Так как входной информацией для f служит только A(i-1), то узнать, поменялось уже A(i-1) функцией copy или еще нет, невозможно. Попытка же ввести для f (аналогично и copy) зависимость типа "отработать, включить copy, отключиться" нереализуема ввиду того, что объект 2-го порядка не способен управлять другим объектом 2-го порядка. Следовательно, и f, и copy существуют и работают одновременно, никогда не отключаясь и не меняя своего алгоритма. Но тогда мы опять приходим к системе обыкновенных, нерекурсивных уравнений: A(i-1)=copy(A(i)); A(i)=f(A(i-1)).

Откуда A(i-1)=f(copy(A(i-1))). А это тоже самое что A(i)=f(A(i)), или A=f(A), оно же A=I(A).

Аналогично в случае произвольной смешанной структуры из нескольких кольцевых структур и объектов класса 2.2:

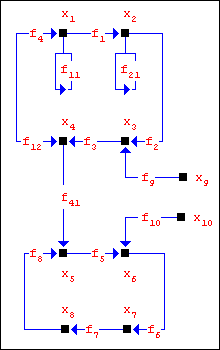
Соответствующая система уравнений (естественно, полагаем, что уравнение связи равно "+"): x₁=f₁₁(x₁)+f₄(x₄); x₂=f₁(x₁)+f₂₁(x₂); x₃=f₂(x₂)+f₉(x₉); x₄=f₁₂(x₁)+f₃(x₃); x₅=f₄₁(x₄)+f₈(x₈); x₆=f₅(x₅)+f₁₀(x₁₀); x₇=f₆(x₆); x₈=f₇(x₇).

Как и в случае с простейшим объектом класса 2.1 все уравнения нерекурсивны. Таким образом, в конечных системах объектов 2-го порядка рекурсивных уравнений не существует. Забегая немного вперед, скажем, что в бесконечных системах на уровне зависимостей глобальных параметров бесконечных логических доменов возникает так называемая квазирекурсия.

Из вышесказанного вытекает, что процесс перехода решений не идет самопроизвольно, а ограничение числа возможных совокупностей состояний объектов 1-го порядка (решений системы уравнений) делает систему дискретной, то есть способной пребывать только в определенных состояниях, а не в любых. Для перехода от одного состояния (решения) системы к другому нужно искусственно изменять состояние хотя бы одного объекта 1-го порядка. Эти изменения должны быть произведены сторонними силами, не входящими в состав объектов системы.

newpoisk.narod.ru, 21 марта 2005 года