7.1.1. Треугольная схема объекта класса 3.1

Интегральная теория создания ИИ

Графическая принципиальная схема объекта 3-го порядка, реализующего случай 3 (2.2 - на входе, 1.1 или 2.1 - на выходе) такова:

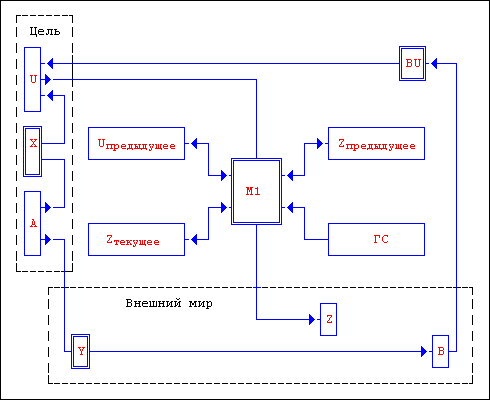
На этой схеме показано принципиальное устройство объекта 3.1. Под внешним миром понимается та среда функционирования, в которой и существует объект 3.1. Цель данного объекта состоит в создании во внешней среде объекта 2-го порядка A->Y->B. Так как A дано изначально, то требуется лишь построить интерпретатор Y и с его помощью менять состояние объекта B. Изначально мы знаем, что должен делать этот объект (каким образом состояние B меняется в зависимости от состояния A). Но нам не известно, каким образом это сделать. Говоря другими словами, мы не знаем, как должен быть устроен интерпретатор Y и каким образом можно управлять объектом B (знать, что собой представляет B и управлять им - далеко не одно и то же). Но как "сказать" объекту 3.1 о том, как мы представляем себе объект A->Y->B. Нужно построить его описание. Так как это объект класса 2.2, то описать мы его можем также объектом класса не ниже 2.2.

Таким объектом-эталоном на нашей схеме служит объект A->X->U (для большей наглядности он очерчен пунктирной линией). Естественно |A|=|U|, |A|=|B|. Такое описание поначалу кажется бессмысленным - ведь в этом случае приходится строить самим объект 2-го порядка. Но на самом деле объект A->X->U хоть и равен по сложности объекту A->Y->B, физически он значительно меньше и построить его гораздо проще, так как он несет лишь информационную нагрузку, в то время как объект A->Y->B строится в основном для роли мощного физического рычага.

Естественно, что нам нужен механизм обратной связи. Уже с самого начала должна быть возможность наблюдать за тем, как эволюционирует объект B. Поэтому объект класса 2.2 B->BU->U также должен быть построен создателями объекта 3.1. Как видно из рисунка, объект U одновременно изменяется как объектом BU, так и объектом X. Среди всех возможных состояний объекта U необходимо выделить некое, так называемое нулевое состояние. Это состояние ничем особо не отличается от других состояний, кроме одного - если все возможные состояния объекта U представить в виде точек в многомерном пространстве, то нулевое состояние должно быть как можно ближе к центру этого пространства. Или говоря по-другому, оно должно представлять собой "среднее арифметическое" возможных состояний, подобно тому как нуль делит координатную ось на две равные части (отсюда и название).

Обозначим выход интерпретатора X за P, а выход BU за Q. Причем если объект B придет в нужное нам состояние, то Q=P. А объект U примет при этом нулевое состояние. Таким образом, чем меньше отличается состояние объекта U от нулевого, тем ближе мы к цели. U служит своего рода индикатором прогресса.

Формирование объекта U (аналогично и U₁ и U₂ в так называемой полной схеме) происходит в виде: U=K₁·(P₁-Q₁)²+K₂·(P₂-Q₂)²+...+K_n·(P_n-Q_n)², где K_i - весовой множитель, показывающий степень важности каждого показателя; он может принимать как положительные, так и отрицательные значения, а также нуль. (P_i-Q_i)² - квадрат разности каждого показателя (P_i и Q_i - значения по i-й оси координат, если рассматривать объекты класса 1.1 P и Q как многомерные переменные). Естественно, что при Q=P мы получим, что P_i-Q_i=0, U также примет нулевое значение. В любом случае U>=0.

M1 - "модуль 1" или базовый модуль. "Модуль 1" - потому что кроме него существуют еще "модуль 2" и "модуль 3", обеспечивающие соответственно подобные и абстрактные построения. Но они работают в более сложных объектах 3-го порядка и в данной схеме опущены. Данный же модуль называется базовым, так как остальные модули строятся на его основе и постоянно используют его в своей работе. Это центральное звено простейшего объекта 3-го порядка, включающее в себя, как видно из схемы, блок движения, блок работы с обратной связью, блок реализации возврата, запоминающее устройство и рабочий орган - объект 1-го порядка Z.

Объекты 1-го порядка U_{предыдущее} и Z_{предыдущее} запоминают соответственно состояния объектов U и Z предыдущего шага. В объекте Z_{текущее} запоминается текущее состояние Z. Это необходимо потому, что на Z кроме объекта 3.1 через универсальный интерфейс воздействуют и остальные объекты внешнего мира. Конечно, они воздействуют и на все остальные части объекта 3.1, но не нужно забывать, что Z должен быть сильно связан с внешним миром, чтобы эффективно на него воздействовать, в то время как остальные части объекта 3.1 связаны с ним слабо. Из-за этого, состояния Z - каким мы его представляем и какое оно на самом деле - сильно различаются. Поэтому перед тем, как изменить Z, M1 записывает его планируемое состояние в Z_{текущее}.

Важную роль играет ГС. Это объект 1-го порядка, число возможных состояний которого должно быть как можно ближе к общему числу состояний (решений) всей системы, то есть S(ГС)->1. В результате чего по отношению к остальным объектам он будет обладать избыточным числом состояний. Одному состоянию некоторого произвольного объекта может соответствовать несколько состояний ГС. Поэтому относительно них его состояния приближенно можно считать случайными. Более конкретно способ постройки объекта Y мы рассмотрим на примере объекта 3.1, построенного по полной схеме.

Число состояний объекта Z меньше числа состояний ГС. Это следует из условия определенности объекта 2-го порядка: Z=M1(...,ГС,...). Поэтому |Z|<=|ГС|, а так как М1 осуществляет работу не только с ГС, то |Z|<|ГС|. Объект Z может быть не одним физически элементарным объектом 1-го порядка, а состоять из нескольких, зачастую весьма несхожих друг с другом, физически элементарных объектов. Фактически в этом случае мы имеем дело с так называемой матрицей эффекторов (смотрите "Объект класса 3.2").

Приведем упрощенный алгоритм работы объекта 3.1: 0. Инициализация: а) Получение значения U; б) U_{предыдущее}:=U; в) Z_{текущее}:=ГС. 1. Получение значения U. 2. Если U=0, то цель достигнута. Перейти на пункт 1. 3. Если U<=U_{предыдущее}, то сделанный шаг оказался удачным (или нейтральным), делаем новый шаг: а) Запоминается состояние U: U_{предыдущее}:=U; б) Запоминается состояние Z_{предыдущее}: Z_{предыдущее}:=Z_{текущее}; в) Случайно генерируется новое состояние Z_{текущее}: Z_{текущее}:=ГС. 4. Если U>U_{предыдущее}, то сделанный шаг оказался неудачным - привел к увеличению значения U, возвращаемся назад: а) Запоминается состояние U: U_{предыдущее}:=U; б) Осуществляется возврат к состоянию Z_{предыдущее}: Z_{текущее}:=Z_{предыдущее}; в) Так как в случае, если и этот шаг окажется неудачным, смысла возвращаться уже нет, то мы не сохраняем Z_{предыдущее}, а присваиваем ему случайное значение: Z_{предыдущее}:=ГС. 5. Делаем шаг - переводим Z в определенное состояние: Z:=Z_{текущее}. Перейти на пункт 1.

В дальнейшем рассмотренную схему мы будем называть треугольной схемой, так как она условно может быть представлена в следующем виде:

A
/ \
/   \
X     Y
/       \
/         \
U-----BU----B

Кроме решения общей задачи - построения объекта 2-го порядка A->Y->B при условии постоянного изменения состояния объекта 1-го порядка A, - объект 3-го порядка может быть применен и для решения частного случая - удерживать состояние объекта B в неизменном виде (противодействуя при этом внешней среде, стремящийся состояние B изменить). Объект A при этом своего состояния не меняет. Назовем этот режим работы объекта 3-го порядка следящим режимом.

Анализируя принцип работы объекта класса 3.1, в частности блока M1, нетрудно заметить, что внутри M1 нужно детальное описание ГС, Z, Z_{предыдущее}, Z_{текущее}. При операциях копирования (Z_{текущее}:=ГС, Z_{предыдущее}:=Z_{текущее} и других) происходит изменение состояния соответствующего объекта 1-го порядка. Эту работу выполняют объекты 2-го порядка. Но вся сложность в том, что ГС, Z, Z_{предыдущее} и Z_{текущее} имеют очень большое число состояний. И поэтому наше представление и о них - их формальная модель - может описывать далеко не все свойства. Следовательно, создавая объекты 2-го порядка для работы с ними, мы сможем учесть только те свойства, что отражены в формальной модели. Возникает ситуация, аналогичная ситуации программирования ЭВМ. Программист, работая с компьютером, не учитывает его механические, тепловые и другие характеристики. Конечно, если формальные модели ГС, Z, Z_{предыдущее} и Z_{текущее} обладают достаточно высоким уровнем (допускают большое количество возможных состояний), с их неполнотой можно смириться, поскольку присутствие универсального интерфейса между Z и внешним миром в принципе позволяет достичь цели даже в таких условиях.

Однако все же желательно уметь манипулировать не частью, а всеми свойствами. Это возможно в случае, когда кроме M1 ни один объект не воздействует на Z, Z_{предыдущее} и Z_{текущее}. Причем Z_{предыдущее} и Z_{текущее} образуют с M1 замкнутую систему, а Z меняется только M1. Возможные связи ГС при этом роли не играют:

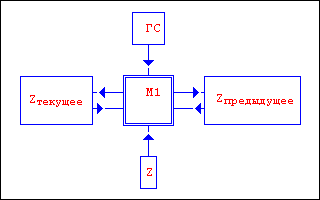
В таком случае в силу существования универсального интерфейса можно утверждать, что состояние Z, Z_{предыдущее} и Z_{текущее} полностью определяются M1. Таким образом, если создателю 3.1 удастся подобрать в состав M1 такие объекты 2-го порядка, что сделают возможным рассматриваемый случай, то ему уже необязательно включать в формальную модель свойства ГС, Z, Z_{предыдущее} и Z_{текущее} в полном объеме. Все будет работать автоматически и с максимальной эффективностью.

newpoisk.narod.ru, 21 марта 2005 года