Теория приливов

Пятая сила

Степень неоднородности гравитационного поля, создаваемого массой m на расстоянии r от нее, можно оценить, используя обычную формулу для гравитационного ускорения: a(r)=-Gmr/r³.

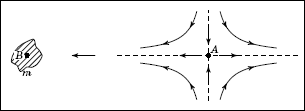
Направление приливных сил в окрестности произвольной
точки A, находящейся вблизи массы m.

Выделим на расстоянии r точку A и определим, на сколько отличается ускорение в точках, удаленных от нее на расстояние Δr (Δr<<r). Используем для этого операцию дифференцирования (Δa/Δr) или, в крайнем случае, разложение с помощью бинома Ньютона (a(r+Δr)˜(r+Δr)^-2). Окажется, что если точка лежит на прямой AB, то разница в ускорениях равна Δa=2GmΔr/r³ и направлена вдоль этой же прямой; а если точка лежит в плоскости, перпендикулярной этому направлению, то Δa=GmΔr/r³ и направлена перпендикулярно прямой AB. О промежуточных случаях дает представление данный выше рисунок. Таким образом, если поместить в точку A какое-либо протяженное тело, то приливные силы будут стараться растянуть его вдоль оси, совпадающей с направлением на возмущающую массу, и сжать в направлениях, перпендикулярных этой оси.

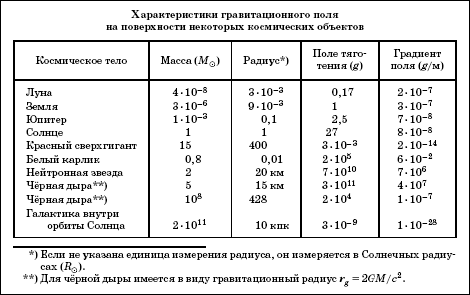
Степень неоднородности гравитационного поля Δa/Δr (или градиент поля) измеряют с помощью специальных приборов - градиентометров. Чувствительность градиентометров, как правило, составляет порядка 10^-7 с^-2, а у лучших их лабораторных образцов - порядка 10^-9 с^-2. Последнее значение даже получило специальное обозначение как единица измерения градиента гравитационного поля: 10^-9 с^-2=1 Этвеш (в честь известного венгерского физика Р.Этвеша). Чтобы оценить величину приливных сил вблизи поверхности некоторых космических тел, обратимся к таблице, где ускорение силы тяготения и градиент поля Δa/Δr даны с помощью величины ускорения силы тяжести на поверхности Земли g=9,8 м/с².

Подчеркнем, что приливное ускорение нельзя "нейтрализовать" никакой невесомостью: даже в свободно пролетающем вблизи поверхности нейтронной звезды космическом аппарате приливные силы разрушат все приборы да и сам аппарат тоже, если его размеры будут превышать 10 сантиметров.

Обычно, говоря о приливных эффектах, одно тело называют возмущающим, а другое - возмущенным. Деление это, конечно, условное. Если нас интересуют приливы в океанах Земли, то возмущенным телом будет Земля, а возмущающими - Луна и Солнце; если же мы интересуемся приливами в лунной коре, то уже Луну считаем возмущенным телом, а Землю - возмущающим (влияние Солнца при этом относительно невелико).

Если небесное тело или одна из его оболочек (атмосфера, гидросфера и тому подобное) легко поддается деформации, то под действием приливной силы их форма изменяется: сферическое тело или какая-либо из его оболочек принимает форму, близкую к вытянутому эллипсоиду. Подчеркивая отличие небесного тела от сферы, иногда говорят, что у него образовались приливные выступы, или горбы. Чтобы оценить степень вытянутости эллипсоида (то есть относительную высоту приливных горбов), сравнивают приливное ускорение и ускорение силы тяготения на поверхности возмущенного тела. Отношение этих ускорений равно 2(R/r)³m/M, где M и R - масса и радиус возмущенного тела, m - масса возмущающего тела и r - расстояние между телами. И если для планет, звезд, галактик эта величина близка к единице, то они заметно изменяют свою форму и могут даже разрушаться.

В общем случае рассчитать приливное воздействие сложно. Обычно рассматривают некоторые предельные ситуации. Например, возмущающее тело принимается за точку, а возмущенное - за однородный эллипсоид, состоящий из несжимаемой жидкости и поэтому легко изменяющий свою форму, но не объем. Такая модель способна описать поведение спутников и небольших планет под действием приливных сил, но не годится в случае планет-гигантов и звезд, плотность которых сильно увеличивается к центру. В этом случае в качестве упрощающей модели используют приближение тела точечной массой, окруженной невесомой оболочкой.

Решая задачу о приливном воздействии, важно знать как изменяется со временем расстояние между телами и их взаимная ориентация. Если они не изменяются или меняются очень медленно, то говорят о статических, или равновесных приливах. Если же тела сблизились на короткое время и вновь удалились друг от друга, то задачу о приливах решают в импульсном приближении, то есть считают, что за время сближения приливные ускорения успели изменить лишь скорости частиц возмущенного тела, но не успели существенно деформировать его. Статическими можно считать приливы на поверхности синхронно вращающихся двойных звезд или, например, земные приливы на Луне. Импульсное приближение обычно используют при исследовании столкновений или близких пролетов в случае галактик, звездных скоплений, кратных звездных систем.

Задачу о статических приливах можно упростить, если считать (как мы это и делали), что расстояние между телами значительно превышает их собственные размеры. Такую задачу в конце 19 века рассмотрел американский астроном Дж.Хилл. Он показал, что однородное тело из несжимаемой жидкости в поле приливных сил принимает форму эллипсоида, вытянутого вдоль направления на возмущающее тело. Если же два тела обращаются вокруг общего центра масс по круговой орбите, то на их форму, помимо приливных сил, влияют и центробежные силы, которые стремятся растянуть тела в плоскости их вращения. Это приводит к тому, что в первом приближении форма жидких тел описывается трехосным эллипсоидом, малая ось которого перпендикулярна орбитальной плоскости. Однако если размеры тел сравнимы с расстоянием между ними, то их форма становится еще более сложной - грушевидной.

Впервые задачу о форме взаимно обращающихся тел решил в 1847-1850 годах французский астроном Э.Рош. Он вычислил, какова будет форма жидкого несжимаемого спутника, движущегося по круговой орбите вокруг точечного массивного тела. Оказалось, что поверхность спутника (форму, которую она примет, обычно называют поверхностью Роша) остается замкнутой, если средняя плотность вещества спутника p больше 3,5M/r³, где M и r - масса центрального тела и радиус орбиты спутника. В случае невыполнения этого условия замкнутой поверхности не существует: сила тяготения спутника не может побороть разрушающее действие приливных и центробежных сил. Максимальное расстояние между массивным телом и спутником, на котором это происходит, называют пределом Роша; очевидно, оно зависит не только от массы планеты, но и от средней плотности спутника. Так, если планета и спутник имеют одинаковую плотность, то предел Роша равен 2,45 радиуса планеты.

Как показали расчеты, жидкий спутник, обращающийся вокруг планеты на предельном расстоянии и вращающийся вокруг своей оси синхронно с орбитальным движением (как Луна вокруг Земли), имеет форму, близкую к трехосному эллипсоиду с отношением осей 1:0,5:0,47. При этом большая ось расположена вдоль направления к планете, а малая - вдоль оси вращения. Напомним, в используемом приближении понятие "жидкий" означает, что тело способно легко изменять свою форму так, чтобы его поверхность везде была перпендикулярна равнодействующей всех приложенных к ней сил. Предполагается при этом, что (помимо молекулярных сил, поддерживающих постоянный объем спутника из несжимаемой жидкости) здесь участвуют только силы тяготения. Однако решение задачи Роша может существенно измениться, если с гравитацией окажутся сравнимы силы светового давления или влияние магнитных полей.

Предположение о равенстве средних плотностей планеты и ее спутников казалось оправданным в середине 19 века, когда о физическом строении спутников было известно очень мало. Сейчас известно, что далеко не всегда спутники планет имеют ту же плотность, что и сами планеты. Еще менее схожи плотности у компонентов двойных звезд. Поэтому удобно сформулировать положение о приливной устойчивости следующим образом: при синхронном обращении по круговой орбите жидкий спутник становится неустойчивым и начинает терять вещество со своей поверхности, если какая-либо часть спутника лежит вне критической полости Роша.

Если суточное вращение спутника или планеты происходит не синхронно с их орбитальным обращением, то, помимо искажения формы тел, возникают новые приливные эффекты. Важнейшими из них являются приливное трение и прецессия оси вращения.

Представим себе, что период суточного вращения планеты короче, чем орбитальный период ее спутника. Тогда приливные горбы вследствие инерционности и вязкости будут опережать направление на спутник. А поскольку притяжение спутника к ближнему горбу сильнее, чем к дальнему, орбитальное движение спутника будет ускоряться, и он станет удаляться от планеты. В свою очередь, планета под действием приливных сил спутника будет замедлять свое вращение. Хотя полный момент вращения в системе "планета-спутник" при этом сохранится, приливное трение, стремясь синхронизовать движение планеты и спутника, приведет к перераспределению вращательного момента между обоими телами.

Второй эффект - прецессия - возникает в том случае, когда ось вращения планеты не перпендикулярна плоскости орбиты спутника. Как мы знаем, в результате суточного вращения планеты она принимает форму эллипсоида, при этом ее можно условно разделить на сферическое тело и экваториальный пояс. И если движение спутника происходит не в плоскости экватора планеты, то приливные силы, приложенные к экваториальному поясу, стремятся развернуть ось вращения планеты. В результате эта ось будет описывать некоторый конус вокруг орбитальной оси спутника. Это и есть явление прецессии.

Часто это явление уподобляют прецессии волчка, вращающегося на столе. Действительно, эти два феномена весьма схожи, однако есть и различия: при одинаковом направлении вращения волчка и планеты, движения их осей происходят в разных направлениях. Вы легко разберетесь, почему это так, если рассмотрите моменты сил, действующих на планету и волчок.

Владимир Георгиевич Сурдин, 2002 год