Таблица умножения "на пальцах"

Шпаргалки для юных математиков

Таблица умножения - необходимые в жизни каждого человека знания, которые требуется элементарно заучить, что на первых школьных порах дается совсем не элементарно. Это потом уже с легкостью мага мы "щелкаем" примеры на умножение: 2·3, 3·5, 4·6 и так далее. С возрастом, правда, все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга. Однако, овладев одной незамысловатой техникой "ручного" умножения, мы можем запросто отказаться от услуг калькулятора. Но сразу уточним, что говорим только о школьной таблице умножения, то есть для чисел от 2 до 9, умножаемых на числа от 1 до 10.

Умножение для числа 9 - 9·1, 9·2 ... 9·10 - легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится "на пальцах". Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).

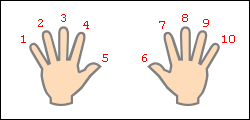
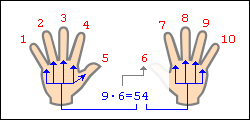
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа - количество единиц. Слева у нас 5 пальцев не загнуто, справа - 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип "вычисления".

Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве "счетной машинки" не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа - 2 клеточки. Значит 9·8=72. Все очень просто.

Теперь несколько слов тем любознательным детям, которые кроме механического применения сказанного хотят понять, из-за чего это работает. Здесь все основано на таком наблюдении, что числу 9 не хватает всего лишь единицы до круглого числа 10, в котором разряд единиц содержит число 0. Умножение можно записать как сумму одинаковых слагаемых. Например, 9·3=9+9+9. Всякий раз, прибавляя следующую девятку, мы знаем, что еще одной единички в ответе не будет доставать до круглого числа. Следовательно, сколько раз прибавлялась девятка (или, по-другому, на какое число x выполнялось умножение), столько же единичек будет не доставать в ответе. Поскольку разряд единиц исчисляет не более 10 чисел (от 0 до 9), а при умножении 9·x=? в разряде единиц не будет хватать ровно x единичек, то и число в разряде единиц будет равно 10-x. Это отражено в примере с руками: мы загибали палец с номером x и для разряда единиц подсчитывали оставшиеся пальцы справа, а на самом деле из 10 пальцев просто исключали пальцы с номерами от 1 до x, выполняя таким образом операцию 10-x.

В то же время с каждой прибавленной девяткой увеличивается на 1 число в разряде десятков, причем изначально этот разряд был пустым (равным нулю). То есть для первой девятки разряд десятков равен нулю, прибавление второй девятки увеличивает его на 1, третьей девятки - еще на 1, и так далее. А значит число десятков равно x-1, поскольку отсчет десятков начинался с нуля. В примере с руками мы загибали палец с номером x, обеспечивая этим действие "минус один", и считали количество пальцев слева от загнутого, а их там оказывается ровно x-1. Таков секрет этой нехитрой методики.

Отсюда следуют дополнительные соображения. Мало того, что пример 9·x=? легко вычислять через число x (разряд десятков равен x-1, разряд единиц равен 10-x), так еще такой пример можно вычислять как x·10-x. Другими словами, дописываем справа к числу x один нулик и вычитаем из получившегося числа число x. Например, 9·5=50-5=45, или 9·6=60-6=54, или 9·7=70-7=63, или 9·8=80-8=72, или 9·9=90-9=81. Таким необычным шагом мы превращаем пример на умножение в пример на вычитание, который значительно проще решается.

Умножение для числа 8 - 8·1, 8·2 ... 8·10 - действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца - с номером x и следующий палец с номером x+1. Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось незагнутых пальцев слева. В-третьих, это напрямую работает при умножении на число от 1 до 5, а при умножении на число от 6 до 10 нужно отнять от числа x пятерку и выполнить расчет как для числа от 1 до 5, а к ответу затем добавить число 40, потому что иначе придется выполнять переход через десяток, что не совсем удобно "на пальцах", хотя в принципе это не так сложно. Вообще надо заметить, что умножение для чисел ниже 9 тем неудобнее выполнять "на пальцах", чем ниже число расположено от 9.

Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 4. Загибаем палец с номером 4 и за ним палец с номером 5 (4+1). Слева у нас осталось 3 незагнутых пальца, значит нам необходимо загнуть еще 3 пальца после пальца с номером 5 (это будут пальцы с номерами 6, 7 и 8). Осталось 3 пальца не загнуто слева и 2 пальца - справа. Следовательно, 8·4=32.

Еще пример: вычислить 8·7=?. Как было сказано выше, при умножении на число от 6 до 10 нужно отнять от числа x пятерку, выполнить расчет с новым числом x-5, а затем добавить к ответу число 40. У нас x=7, значит загибаем палец с номером 2 (7-5=2) и следующий палец с номером 3 (2+1). Слева один палец остался не загнут, значит загибаем еще один палец (с номером 4). Получаем: слева 1 палец не загнут и справа - 6 пальцев, что обозначает число 16. Но к этому числу нужно еще добавить 40: 16+40=56. В итоге 8·7=56.

И на всякий случай разберем пример с переходом через десяток, где никаких пятерок предварительно вычитать не нужно и никаких 40 после прибавлять тоже не нужно. Вдруг вам так окажется проще. Попробуем вычислить 8·8=?. Загибаем два пальца с номерами 8 и 9 (8+1). Слева осталось 7 незагнутых пальцев. Запомним, что у нас уже есть 7 десятков. Теперь начинаем справа загибать 7 пальцев. Поскольку там остался только один незагнутый палец, загибаем его (осталось еще 6 загнуть), затем переходим через десяток (это значит, что все пальцы разгибаем), и загибаем слева направо 6 недозагнутых пальцев. Справа осталось 4 пальца не загнуто, значит в разряде единиц в ответе будет число 4. Ранее мы запомнили, что было 7 десятков, но так как нам пришлось перейти через десяток, то один десяток нужно отбросить (7-1=6 десятков). В итоге 8·8=64.

Дополнительные соображения: здесь также можно вычислять примеры просто через число x в форме выражения на вычитание x·10-x-x. То есть дописываем справа к числу x один нулик и два раза вычитаем из получившегося числа число x. Например, 8·5=50-5-5=40, или 8·6=60-6-6=48, или 8·7=70-7-7=56, или 8·8=80-8-8=64, или 8·9=90-9-9=72.

Умножение для числа 7 - 7·1, 7·2 ... 7·10. Здесь без переходов через десяток не обойтись. Числу 7 на хватает тройки до круглого числа 10, следовательно загибать придется сразу по 3 пальца. Сразу же запоминаем получившееся количество десятков по количеству незагнутых слева пальцев. Следом справа загибается столько пальцев, сколько насчитано десятков. Если во время загибания пальцев требуется переход через десяток, делаем его. Затем второй раз загибается столько же пальцев, то есть одна операция выполняется два раза. И вот теперь количество оставшихся справа незагнутых пальцев записывается в разряд единиц, количество ранее насчитанных десятков (минус количество переходов через десяток) - в разряд десятков.

Видите, как тут уже становится сложнее посчитать "на пальцах", чем выудить эти сведения из памяти. И потом, для чисел 7, 8 и 9 забывчивость элементов таблицы умножения еще как-то оправдательна, но для чисел ниже грешно не помнить. Потому на этом месте остановим рассказ в надежде на то, что саму нить "вычислений" вы ухватили и, если будет на то крайняя надобность, сможете самостоятельно спуститься к числам ниже 7, хотя человек, считающий "на пальцах" нечто в духе "пятью пять", должно быть, выглядит крайне глупо.

Дмитрий Сахань, 21 мая 2005 года