Пифагоровы штаны на все стороны равны

Шпаргалки для юных математиков

Это язвительное замечание (которое в полном виде имеет продолжение: чтобы это доказать, нужно снять и показать), придуманное кем-то, по-видимому, потрясенным внутренним содержанием одной важной теоремы евклидовой геометрии, как нельзя точно раскрывает отправную точку, из которой цепь совсем несложных размышлений быстро приводит к доказательству теоремы, а также к еще более значимым результатам. Теорема эта, приписываемая древнегреческому математику Пифагору Самосскому (6 век до нашей эры), известна чуть ли не каждому школьнику и звучит так: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Пожалуй, многие согласятся, что геометрическая фигура, обозванная шифровкой "пифагоровы штаны на все стороны равны", называется квадратом. Ну и с улыбкой на лице добавим безобидной шутки ради, что имелось в виду в продолжении шифрованного сарказма. Итак, "чтобы это доказать, нужно снять и показать". Ясно, что "это" - под местоимением подразумевалась непосредственно теорема, "снять" - это получить в руки, взять названную фигуру, "показать" - имелось в виду слово "покасать", привести в соприкосновение какие-то части фигуры. Вообще "пифагоровыми штанами" окрестили напоминавшую по виду штаны графическую конструкцию, получавшуюся на чертеже Евклида при весьма сложном доказательстве им теоремы Пифагора. Когда нашлось доказательство проще, быть может, какой-то рифмоплет сочинил эту скороговорку-подсказку, чтобы не запамятовать начало подхода к доказательству, а народная молва уж разнесла ее по свету как пустую поговорку.

Так вот если взять квадрат, и внутрь него поместить меньший квадрат так, чтобы центры их совпадали, и повернуть притом меньший квадрат до соприкосновения его углов со сторонами большего квадрата, то на большей фигуре окажутся выделены сторонами меньшего квадрата 4 одинаковых прямоугольных треугольника.

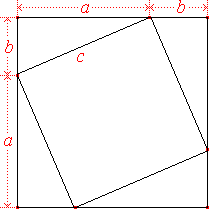
Отсюда уже лежит прямой путь к доказательству известной теоремы. Пусть сторону меньшего квадрата обозначим через c. Сторона большего квадрата равна a+b, и тогда его площадь равна (a+b)²=a²+2ab+b². Ту же площадь можно определить как сумму площади меньшего квадрата и площадей 4 одинаковых прямоугольных треугольников, то есть как 4·ab/2+c²=2ab+c². Поставим знак равенства между двумя вычислениями одной и той же площади: a²+2ab+b²=2ab+c². После сокращения членов 2ab получаем вывод: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов, то есть a²+b²=c².

Слово о числе пифагоровом

Сразу не каждый поймет, какой прок от этой теоремы. С практической точки зрения ее ценность состоит в служении базисом для многих геометрических вычислений, как например определения расстояния между точками координатной плоскости. Из теоремы выводятся некоторые ценные формулы, ее обобщения ведут к новым теоремам, перекидывающим мостик от вычислений на плоскости до вычислений в пространстве. Следствия теоремы проникают в теорию чисел, открывая отдельные подробности структуры ряда чисел. И многое другое, всего не перечислишь.

Взгляд с точки зрения праздного любопытства демонстрирует преподношение теоремой занимательных задачек, формулируемых до крайности понятно, но являющихся подчас крепкими орешками. В пример достаточно привести наиболее простую из них, так называемый вопрос о пифагоровых числах, задаваемую в бытовом изложении следующим образом: можно ли построить комнату, длина, ширина и диагональ на полу которой одновременно измерялись бы только целыми величинами, скажем шагами? Всего лишь малейшее изменение этого вопроса способно сделать задачу чрезвычайно сложной. И соответственно, найдутся желающие чисто из научного задора испытать себя в раскалывании очередного математического ребуса. Другое изменение вопроса - и еще одна головоломка. Часто в ходе поиска ответов на подобные проблемы математика эволюционирует, приобретает свежие взгляды на старые понятия, обзаводится новыми системными подходами и так далее, а значит теорема Пифагора, впрочем как и любое другое стоящее учение, с этой точки зрения имеет не меньшую пользу.

Коль уж речь зашла о вопросе пифагоровых чисел - троек натуральных (целых положительных) чисел, удовлетворяющих решению пифагорова уравнения a²+b²=c², - необходимо отметить, что задача эта была решена самими пифагорейцами, причем их решение позволяло отыскивать все тройки взаимно простых (то есть не имеющих общих делителей) пифагоровых чисел по формулам: a=m²-n², b=2mn, c=m²+n², где m и n - натуральные числа разной четности и с условием m>n (чтобы не иметь отрицательного или нулевого значения a). Для примера найдем первую тройку при m=2 и n=1: a=2²-1²=3, b=2·2·1=4, c=2²+1²=5, следовательно 3²+4²=5².

Математика времен Пифагора не признавала иных чисел, кроме рациональных (натуральных чисел или дробей с натуральным числителем и знаменателем). Все измерялось целыми величинами или частями целых. Потому так понятно стремление делать геометрические вычисления, решать уравнения все больше в натуральных числах. Пристрастие к ним открывает путь в невероятный мир таинства чисел, ряд которых в геометрической интерпретации первоначально вырисовывается как прямая линия с бесконечным множеством отметин. Иногда зависимость между какими-то числами ряда, "линейным расстоянием" между ними, пропорцией тотчас бросается в глаза, а иной раз самые сложные мыслительные конструкции не позволяют установить, каким закономерностям подчинено распределение тех или иных чисел. Выясняется, что и в новом мире, в этой "одномерной геометрии", старые задачи сохраняют силу, меняется лишь их постановка. Как например, вариант задания о пифагоровых числах: "От дома отец делает x шагов по x сантиметров каждый, а затем идет еще y шагов по y сантиметров. За ним шагает сын z шагов по z сантиметров каждый. Какими должны быть размеры их шагов, чтобы на z-том шаге ребенок вступил в след отца?"

Пифагору, да и пифагорейцам в целом, приписывают изучение свойств целых чисел. Вряд ли это было иначе, хотя бы уж потому, что вывод формул поиска пифагоровых троек требует как минимум маломальского представления о целых числах. Верно и обратное: получение этих формул дает понимание связей между квадратами натуральных чисел. Во всяком случае, если некое число представить суммой натуральных чисел m+n, то его квадрат отличается от суммы квадратов m²+n² на величину 2mn. Однако последняя сумма может и не быть квадратом числа. А вот возведенная в квадрат, точно будет: (m²+n²)². Величина 2mn может вообще не быть квадратом числа, но только не возведенная в квадрат: (2mn)². В свою очередь квадрат другого числа, представленного разницей m-n, отличается от суммы m²+n² снова на величину 2mn. Следовательно, произведение исходных чисел, то есть (m+n)(m-n)=m²-n², опять может не оказаться квадратом числа. Но таковым неизбежно окажется возведенное в квадрат: (m²-n²)². В конце концов получается (m²-n²)²+(2mn)²=(m²+n²)², что и составляет полную формулу целочисленного решения пифагорова уравнения.

Сложно ли теперь сообразить, что квадрат суммы квадратов представим суммой квадратов? Или что квадрат разницы квадратов - разницей квадратов. Или что квадрат произведения - разницей квадратов суммы квадратов и разницы квадратов. В отношении последнего утверждения вспомните формулу преобразования произведения: ab=(a+b)²/2²-(a-b)²/2² и сравните, сколь общего у нее с формулой (2mn)²=(m²+n²)²-(m²-n²)². На самом деле из теоремы Пифагора косвенно или напрямую вытекает слишком много важных математических утверждений, рассказывать о чем можно очень долго.

По затерявшимся стопам древних математиков

Справедливости ради полагается отметить некоторую сложность для начинающего математика пифагорейской методики развития мысли. Это особого рода стиль математического мышления, к нему нужно привыкать. Интересен один момент. Математики вавилонского государства (оно возникло задолго до рождения Пифагора, почти полторы тысячи лет до него) тоже, видимо, знали какие-то методы поиска чисел, которые впоследствии стали называться пифагоровыми. Были найдены клинописные таблички, где вавилонские мудрецы записали выявленные ими тройки таких чисел. Некоторые тройки состояли из чересчур больших чисел, в связи с чем наши современники стали предполагать наличие у вавилонян недурственных, и вероятно даже немудреных, способов их вычисления. К сожалению, ни о самих способах, ни об их существовании ничего не известно.

Если вам не чужд дух исследовательских приключений, есть предложение мысленно ступить на запыленные в глубине веков научные тропинки и поискать этот артефакт древних времен, или простым языком выражаясь, ответить на вопрос, могли ли в Вавилоне в принципе иметь иную схему вычислений, возможно более легче пифагорейской (для последней требуется: 2 возведения в квадрат, 2 умножения, сложение и вычитание).

Итак, сперва вообразим, будто когда-то в прошлом был задан вопрос сродни следующей современной постановке: на сколько отличаются квадраты соседних натуральных чисел? Скорее всего вавилоняне смогли бы ответить, что эти квадраты отличаются на величину (a+1)²-a²=a²+2a+1-a²=2a+1. Число 2a+1 есть число нечетное, а среди нечетных чисел существует бесконечное множество квадратов чисел. Следовательно, обязательно найдется такое a, при котором 2a+1=b². Какой-нибудь пример: a=12, 2·12+1=5². Таким образом, уравнение a²+b²=(a+1)² имеет нескончаемое множество решений в натуральных числах.

Разумеется, поиск подобных решений предельно прост, и для распространенной записи a²+b²=c² выполняется по следующим формулам: b есть произвольное нечетное число, большее единицы, a=(b²-1)/2, c=a+1.

Например, хотим чтобы b=31, тогда a=(31²-1)/2=(961-1)/2=480, c=480+1=481. Вот оно решение: 480²+31²=481². Если же захотим числа побольше, допустим b=123456789, тогда a=(123456789²-1)/2=7620789375095260, c=7620789375095260+1=7620789375095261. Вот и это решение: 7620789375095260²+123456789²=7620789375095261².

Вообразим теперь, будто вавилоняне пошли дальше и задали себе нечто в таком духе: какова разница между квадратами несмежных натуральных чисел? Очевидно, (a+n)²-a²=a²+2an+n²-a²=2an+n²=n(2a+n). Для выражения в скобках, способного описать всякое большее n и одинаковое с ним четностью число, опять найдутся такие a и n, при которых умножение внутрискобочного числа на n даст квадрат. Какой-нибудь пример: a=8, n=9, 9·(2·8+9)=15². Поэтому уравнение a²+b²=(a+n)² тоже обладает бесчисленным множеством целочисленных решений.

Укажем формулы поиска таких решений опять же для распространенной записи a²+b²=c²: b=nm (из соображений b²=n(2a+n)=n²m², если принять 2a+n=nm²), a=n(m²-1)/2, c=a+n. Непременное условие: 0<n<m и четность m и n совпадает.

Например, хотим чтобы n=3 и m=5, тогда b=3·5=15, a=3·(5²-1)/2=36, c=36+3=39. Вот решение: 36²+15²=39². Пример с большими числами: хотим чтобы n=123 и m=567, тогда b=123·567=69741, a=123·(567²-1)/2=19771512, c=19771512+123=19771635. Вот решение: 19771512²+69741²=19771635².

В общем, находить пифагоровы числа можно не только пифагорейским способом. С этим вопросом закончили. Напоследок хочется отметить пару выводов, какие следует из числа b=nm с указанными условиями на числа m и n. Во-первых, наименьшее возможное целочисленное решение пифагорова уравнения не имеет смысла искать при b<3, так как 3 - наименьшее число, которое можно представить произведением разных чисел одинаковой четности. Во-вторых, если b простое число (не разлагаемое в произведение простых множителей), то здесь всегда c=a+1, ведь в этом случае n=1 и m=b. Однако это вовсе не означает, что во всяком целочисленном решении уравнения a²+b²=(a+1)² число b будет простым, ибо составное число тоже представимо произведением единицы на само число (то есть когда n=1 и m=b).

Дмитрий Сахань, 23 июля 2006 года