На чем могла держаться уверенность Пьера Ферма?

Шпаргалки для юных математиков

Кто не слышал названия Великая теорема Ферма, тот не знает о знаменитом математическом утверждении, высказанном в середине 17 века французским монахом, талантливым математиком-самоучкой Пьером Ферма. В математическом плане утверждение гласило: невозможно решить в натуральных числах уравнение, аналогичное уравнению Пифагора, если показатель степени станет больше 2. Рядом со своим замечанием Ферма приписал, что знает поистине удивительное тому подтверждение, но поля книги "Арифметика" Диофанта, где рукой Ферма было поставлено это замечание, видите ли малы Пьеру, чтобы записать доказательство.

Ситуация с Ферма-математиком полна драматизма. Наш современник выскажется о нем как о великом математике, благодаря чьим основополагающим трудам прошло становление теории чисел. Современник Ферма, напротив, склонился бы к критике в разговоре о математических способностях Пьера. Какой же это великий математик, кто тридцати лет отроду осваивает базис, которым каждый математик владеет с пеленок. История с овладением базисом, но теперь в отношении свойств чисел, еще раз повторяется позже, годам к 40 возраста Ферма. Критик выразил бы недовольство неповторимой манерой Пьера общаться с именитыми математиками на уровне безвредных колкостей в виде периодически подбрасываемых трудных задачек, о решении которых Ферма заявлял безапелляционно.

Удивителен Ферма в своей категоричной правоте и беспечности в ее засвидетельствовании. Он открывает невероятные по тем временам вещи, но часто не указывает систему доказательства целиком. Словно его интерес основан на поиске истины ради поиска. Знаменитое замечание сделано было в форме личной отметины о благополучном решении простой задачи. Сколько же математических умов в дальнейшем было взбудоражено этим вызовом. Математики следующих поколений раз за разом соприкасались с проблемами, якобы решенными Пьером Ферма. Каждое его твердое заявление, его невообразимые теоремы подтверждались изысканием безупречных доказательств. Пока, наконец, не осталась последняя недоказанная теорема, источавшая дух авантюрной проницательности ума ее автора. В этот раз события повторили прежний ход: Великая теорема Ферма была доказана.

Понадобилось почти 400 лет, прежде чем Эндрю Уайлс, профессор математики Принстонского университета, в 1995 году представил общественности сложное окончательное доказательство объемом во много страниц убористого математического текста, воспользовавшись при этом теорией эллиптических кривых. С этого момента математики разделились на два лагеря: твердолобых скептиков и романтических оптимистов, рассказывает Саймон Сингх в своей книге "Великая теорема Ферма". Первые убеждены в ложности или ошибочности заявления Ферма о нахождении им доказательства. Вторые уверены в существовании какого-то тонкого аргумента, сводящего доказательство теоремы Ферма к простому и который с самого начала ускользнул от всех причастных к поиску доказательства.

Путь Эндрю Уайлса

Как-то в середине 20 века начинающие японские математики Ютака (Тойо) Танияма и Горо Шимура, занимаясь исследованием модулярных форм (специфичные математические объекты, обладающие высочайшим уровнем симметрии), выдвинули неожиданную гипотезу о том, что каждой модулярной форме можно поставить в соответствие определенную эллиптическую кривую.

Комментарий о модулярных формах: Квадрат на плоскости, перпендикулярной взгляду наблюдателя, можно повернуть вокруг его центра на 90, 180, 270 и 360 градусов, и в новом положении он будет неотличим от прежнего. Это вращательная симметрия. Круг на той же плоскости можно поворачивать вокруг его центра на любой градус, в новом положении он также будет неотличим от прежнего; уровень вращательной симметрии круга несравнимо выше. Квадрат можно перевернуть вокруг его центральных осей и диагоналей, и снова он станет неотличим от прежнего. Это зеркальная симметрия. Ее уровень у круга опять много выше: круг неотличим от прежнего в результате переворота вокруг его центральной оси при любом ее наклоне. Однако эти формы не обладают трансляционной симметрией, то есть при сдвиге фигуры наблюдатель заметит отличие между начальным и конечным положением. Разные объекты - плоские ли это формы, объемные ли они - обладают различным набором симметрий и имеют разные их уровни. Существуют и такие вычурные формы, с причудливыми и невообразимыми в мыслях изгибами своей поверхности, которые можно поворачивать, переворачивать, переставлять фрагменты, сдвигать и так далее, короче говоря, преобразовывать бесконечным множеством дозволенных способов, и при этом они останутся неотличимыми от прежнего положения. Вот такие объекты и называются модулярными формами.

В прямом смысле гипотеза Таниямы и Шимуры означала следующее: поверхность всякого такого объекта, который называют модулярной формой, обязательно задана некоторой функцией, кубическим уравнением, соответствующим какой-то эллиптической кривой. Тогда немецкий математик Герхард Фрей попытался получить из уравнения Ферма кубическое уравнение, для этой цели намеренно рассматривая случай ошибочности Великой теоремы Ферма. И выходило так, что преобразованному уравнению не соответствует ни одна модулярная форма, то есть воображаемый объект, определенный полученной эллиптической кривой, не обладает должной симметрией модулярной формы, чего не могло быть по гипотезе японских математиков. Следовательно, если бы удалось доказать ту гипотезу, Великая теорема Ферма автоматически получала бы доказательство. Что и сделал англичанин по происхождению Эндрю Уайлс, окончательно завершив свою нелегкую работу в 1995 году.

Подробнее обсуждать нюансы его математической мысли мы не станем, так как это, во-первых, потребует глубокого погружения в чрезвычайно сложные для школьного уровня математические представления, а во-вторых, эти мысли на самом деле имеют лишь косвенное касательство к теореме Ферма, так как в основном нацелены на доказательство гипотезы Таниямы-Шимуры (и это гораздо более полезный результат, чем просто доказательство теоремы Ферма; а истинность последней вообще-то обеспечивалась сопутствующим подтверждением немодулярности эллиптической кривой Герхарда Фрея). Поэтому перейдем сразу к вероятным идеям Пьера Ферма. Лишний раз подчеркнем, нижеследующий материал - всего-навсего его возможные мысли или их отголоски, простая игра воображения, некие наброски и намеки. Стопроцентного доказательства здесь искать не нужно, хотя некоторые выкладки и соображения могут оказаться полезными просто как опорные схемы для каких-то иных целей.

Ход Ферма: несуществующая степень пифагоровых чисел

Из исторических справок о Пьере Ферма нам сегодняшним в отдельных подробностях известен его путь самостоятельного углубления в мир математических таинств. Книга "Арифметика" Диофанта, которую Ферма тщательным образом штудировал поначалу из досужего интереса, оказала, видимо, самое значительное направляющее влияние на все дальнейшие исследования этого необычного математика-самоучки. В числе прочих вопросов, затрагиваемых в означенной книге, рассматривалось пифагорово уравнение и методы его решения в натуральных числах (эти решения - тройки чисел - еще называют пифагоровыми числами). В отношении последних информация сводилась к главному результату: всякое решение уравнения a²+b²=c² можно найти по формулам a=k(2pq), b=k(p²-q²), c=k(p²+q²), где p и q - натуральные числа разной четности, число k - некоторый общий натуральный множитель. То есть исходное уравнение в среде натуральных чисел может принимать вид (k2pq)²+(kp²-kq²)²=(kp²+kq²)². В исследовании вопросов, связанных с данным видом пифагорова уравнения, зачастую достаточно ограничиться рассмотрением возможных решений только во взаимно простых числах, исключив тем самым общий множитель k, что сделаем и мы.

Так вот, на некотором этапе осмысления пифагорова уравнения Пьер Ферма способен был задать себе вопрос: а могут ли в указанных формулах числа a, b и c одновременно оказаться квадратами, кубами, биквадратами или более высшими степенями каких-то целых чисел? В буквальном смысле это означало постановку вопроса о решаемости в натуральных числах следующей системы из 3 уравнений: aⁿ=2pq, bⁿ=p²-q², cⁿ=p²+q² (из этой системы следует: cⁿ+aⁿ=(p+q)², cⁿ-aⁿ=(p-q)², cⁿ+bⁿ=2p², cⁿ-bⁿ=2q², cⁿ+aⁿ+bⁿ=2p(p+q), cⁿ-aⁿ-bⁿ=-2q(p-q), cⁿ+aⁿ-bⁿ=2q(p+q), cⁿ-aⁿ+bⁿ=2p(p-q)). В действительности такая система имеет натуральные решения только для n=1. Отсюда Пьер Ферма смог бы сделать первый вывод: вариация пифагорова уравнения (aⁿ)²+(bⁿ)²=(cⁿ)² не решается в натуральных числах при n>1. Кстати, случай n=2 - это уравнение a⁴+b⁴=c⁴, доказывать отсутствие натуральных решений у которого Пьер Ферма умел совершенно иным образом, о чем сообщают страницы истории. Вывод второй касается уже нечетных степеней, больших единицы (вообще достаточно ограничиться лишь нечетными простыми степенями): если даже уравнение (a^m)ⁿ+(b^m)ⁿ=(c^m)ⁿ при оговоренных степенях n имеет гипотетическое натуральное решение, его числа не могут быть одновременно никакими четными степенями m.

На первый взгляд прогресс незначительный. Однако мысли, подобные изложенным, могли бы придать больше уверенности Пьеру Ферма в своей позиции еще задолго до окончательного формулирования его диковинной теоремы. Во всяком случае уже подтверждалась нерешаемость уравнения при любых четных составных степенях, для прочих степеней гарантировалось отсутствие решений в квадратах, биквадратах, бикубах и так далее.

Ход 2: нечетная степень несуществующего трехчлена

Итак, полет фантазии ведет нас к очередному измышлению, начальной сценой которого станет эта: Пьер Ферма устремляет внимание на случаи нечетных простых степеней, доказательство целочисленной решаемости или нерешаемости уравнений с которыми степенями снимет оставшиеся вопросы.

Есть такая теорема о делении двучлена aⁿ+bⁿ на a+b, если степень n нечетная. Думается, Пьеру Ферма было по силам получить подобный результат самостоятельным образом и применить его в деле: если уравнение записать в виде a^p+b^p=(a+b-d)^p (где d - подходящее натуральное число и p - нечетная простая степень), тогда обе части равенства должны делиться на a+b и одновременно на трехчлен a+b-d. Отсюда следует или делимость d нацело на a+b - это первый вариант, или делимость d^p так же нацело на a+b - это второй вариант.

Первый вариант, в котором число d наряду с прочими возможными простыми множителями, например совокупно обозначаемыми символом m, включает в себя еще и абсолютно все простые множители двучлена a+b, очевидно абсурдный: если d=m(a+b), то вместо трехчлена a+b-d получаем a+b-m(a+b)=(a+b)(1-m), где или m=0 (и тогда имеется неверное равенство a^p+b^p=(a+b)^p), или m действительно являет собой произведение некоторых простых множителей, но вследствие этого трехчлен a+b-d выходит не натуральным числом.

Второй вариант выявляет сразу две необычные подробности: число d наряду с прочими возможными простыми множителями непременно должно включать в себя еще и все (по их перечислению и без абсолютного совпадения их показателей) простые множители двучлена a+b (причем включает в себя те множители таким образом, чтобы при возведении в степень p быть способным делиться на этот двучлен), и во-вторых, число d должно делиться нацело на степень p, то есть хотя бы один простой множитель p должен входить в число d.

Первая подробность, таким образом, свидетельствует о существенных ограничительных условиях на числа d и a+b и для любого значения нечетной простой степени p немедленно опровергает всякую возможность натуральных решений, где бы a+b равнялось какому-то простому числу или какому-то составному числу со всеми единичными показателями его простых множителей.

Для сравнения: Среди натуральных решений пифагорова уравнения бесконечно много таких, в которых a+b есть простое или же высказанное выше составное число, и d при этом делится на степень 2, то есть удовлетворяет требованию второй подробности, хотя при том требование первой подробности вовсе не обязано удовлетворяться в части включения в себя всех простых множителей суммы a+b (что объяснимо переходом на случай четной простой степени). Например, решения 3²+4²=(3+4-2)², 5²+12²=(5+12-4)², 8²+15²=(8+15-6)², 27²+36²=(27+36-18)², 60²+91²=(60+91-42)² и многие другие; перечень их можно продолжать до бесконечности.

Надо отметить, если первая деталь само собой очевидна, вторая подробность сначала не выглядит бесспорной, однако она подтверждается одной важной теоремой теории чисел, сформулированной тем самым Пьером Ферма: выражение a^p-a с натуральным числом a обязательно делится на p, если p - простое число (та же теорема в иной форме: натуральное число a^p при делении на простое число p даст тот же остаток, который даст a/p). То есть левая часть уравнения a^p+b^p=(a+b-d)^p при делении на p даст остаток как у (a+b)/p, правая часть - остаток как у (a+b-d)/p; следовательно d не может не делиться на p.

Мысль вслух: Очень может быть, своим появлением упомянутая теорема о простых числах в немалой мере обязана исследованиям, проводимым Пьером Ферма над злополучной модификацией пифагорова уравнения.

Проиллюстрировать действительность второй подробности можно и другим манером. Для примера возьмем случай простой степени p=3 (нетрудно доказать адекватность следующих соображений для всякой нечетной простой степени исходя из разложения a^p+b^p=(a+b)(a^p-1+b^p-1-ab(a^p-3+b^p-3-ab(...a²+b²-ab))), следуемого из указанной выше теоремы о делении двучлена aⁿ+bⁿ на a+b при нечетном n). Так вот пусть дано a³+b³=(a+b-d)³. По формуле бинома Ньютона раскроем скобки, а в левой части равенства вынесем за скобки a+b: (a+b)(a²+b²-ab)=(a+b)³-3(a+b)²d+3(a+b)d²-d³. Если предполагается возможным d³=m(a+b), тогда обе части равенства сокращаются на a+b: a²+b²-ab=(a+b)²-3(a+b)d+3d²-m. Теперь раскроем первые скобки: a²+b²-ab=a²+2ab+b²-3(a+b)d+3d²-m. Сократим члены a² и b² и перенесем 2ab в левую часть: -3ab=-3(a+b)d+3d²-m. Так как левая часть делится на p=3, то m в правой части тоже должен делиться на p=3, а значит d изначально включал в себя этот множитель. Более того, на основе последнего заключения и выражения 3ab=3(a+b)d-3d²+m можно доказать, что или a, или b неизбежно делится на p=3, или же они оба делятся на этот показатель, но тогда в последнем эпизоде это уже будет случай не взаимно простых чисел.

Таким образом, отсекая решения не во взаимно простых числах, приходится признать по крайней мере следующее более полное соображение: если число d неизбежно включает в себя хотя бы один или даже несколько (обозначим это количество символом x) множителей p, и также снова неминуемо включает в себя множители двучлена a+b, которые бы при возведении в степень p давали m(a+b), и наконец всего лишь возможно включает в себя какие-то прочие множители (обозначим их символом n), тогда d^p=(p^x)^pn^pm(a+b). Далее можно переписать равенство a^p+b^p=(a+b-d)^p как a^p+b^p=(d^p/(p^x)^pn^pm-d)^p и установить тем самым, что m и a+b сами должны быть p-ыми степенями каких-то целых чисел, то есть здесь m^1/p и (a+b)^1/p есть натуральные числа.

Из серии занятных размышлений: Возьмем изучаемое уравнение a^p+b^p=(a+b-d)^p для нечетной простой степени p и прологарифмируем его (пусть основание логарифма обозначим символом m): log_m(a+b)(a^p-1+b^p-1-ab(a^p-3+b^p-3-ab(...a²+b²-ab)))=plog_m(a+b-d). Отсюда log_m(a+b)^1/p+log_m(a^p-1+b^p-1-ab(a^p-3+b^p-3-ab(...a²+b²-ab)))^1/p=log_m(a+b-d). А если основание m=a+b-d? А если m=a+b? А если m=a^p-1+b^p-1-ab(a^p-3+b^p-3-ab(...a²+b²-ab)))?

Еще один любопытный результат: Если a^p+b^p=c^p имеет какое-нибудь натуральное решение, соответственно можно представить уравнение как (c-q)^p+(c-s)^p=c^p, где q и s - подходящие натуральные числа, или конкретно в числах - q=c-a, s=c-b. Так вот для всякого потенциального решения исходного уравнения будет одновременно выполняться равенство q^p+s^p=cn, то есть сумма p-ых степеней разницы между c и a и между c и b непременно делится нацело на c. Доказывается это просто: (c-a)^p+(c-b)^p=....-a^p+....-b^p=cn, где многоточием обозначены члены разложения по формуле бинома Ньютона, которые точно включают в себя множитель c; но ведь из начальных условий -a^p-b^p=-c^p, следовательно и сумма этих отрицательных членов также включает в себя множитель c.

Короче говоря, с каждым новым доводом воображаемый список возможно существующих натуральных решений сильно сокращается. В конце концов, получая все более и более детальное представление о числе d, о котором разговор велся выше, неудивительно что Пьер Ферма в некоторый момент мог определенно заявить: у этого уравнения для степени выше 2 вообще не существует натуральных решений. Во всяком случае объединение изложенных мыслей в некую общую дает кое-что для понимания: рассматривая случай нечетной простой степени p и приняв a=c-q, b=c-s и воспользовавшись a^p+b^p=(a+b-d)^p, имеем (c-q)^p+(c-s)^p=(c-q+c-s-d)^p, откуда следуют факты целочисленной делимости: для упомянутых недавно членов левой части уравнения - это будет -q^p-s^p=-n(2c-q-s-d), и для упоминавшегося ранее члена правой части - это d^p=m(2c-q-s). Легко найти d: d=2c-q-s-(q^p+s^p)/n. Но d^p делится нацело на 2c-q-s, следовательно или (q^p+s^p)/n делится на 2c-q-s, что ведет к ненатуральному решению, или (q^p+s^p)^p/n^p делится на 2c-q-s.

Дифференциал при ненатуральном приращении аргумента

А сейчас вернемся к начальной сцене и дадим волю фантазии развиваться в другом, лишь отчасти фантастическом для того времени направлении. Целью этого игривого поворота станет тема, скажем так, для многих школьников скучная и непонятная. Поэтому аура Великой теоремы Ферма сослужит здесь службу всего-навсего красочного оформления к некоторым важным понятиям затрагиваемой темы. Мы только слегка коснемся этих понятий, и то лишь отдельных из них, чтобы отложить в памяти зерна предстоящих ростков знаний, образовать питательную среду для оптимального формирования будущих представлений о дифференциальном исчислении.

Итак, Пьеру Ферма, при его-то способностях рассудительно созерцать математические соотношения, очевидно не стоило бы усилий заметить, что в уравнении aⁿ+bⁿ=cⁿ каждый из трех членов являет собой пример одной и той же показательной функции, отчего уравнение можно было бы записать в форме ƒ(a)+ƒ(b)=ƒ(c), где функция ƒ задана n-ой степенью аргумента функции. Можно было бы пойти дальше и сформулировать понятную задачу на основе записи знаменитого уравнения в только что предложенной форме: пусть имеется функция y=ƒ(x)=xⁿ и пусть есть такие три натуральных значения x_a, x_b, x_c ее аргумента, для которых верно равенство ƒ(x_a)+ƒ(x_b)=ƒ(x_c); требуется ответить, может ли это равенство быть справедливым при натуральном n>2.

Следует, впрочем, немедленно уточнить: Пьер Ферма не знал понятий функции, производной, дифференциала, предела и приращения, хотя одна из его теорем стала начальной теоремой дифференциального исчисления, устанавливая связь между поведением функции и значением ее производной. Просто во времена Ферма понимание функции как зависимости между переменными величинами, одну из которых многими годами позже стали называть аргументом функции, а другую величину (зависимую от первой) - значением функции, уже витало в воздухе. В полноценное же понятие оно оформилось только в конце 17 века, давая вслед за собой жизнь понятиям приращения (относительного изменения переменной), дифференциала (основной части относительного изменения переменной) и производной (скорости изменения переменной).

Поистине изумительно, что еще десятками лет ранее Пьер Ферма задавался соображениями о производной и ее связи с функцией, излагая свои мысли и методы не теми словами, как это делается сегодня. Главное - суть была идентичной нынешним представлениям. Поэтому мы можем оказаться с большим процентом вероятности недалекими от истины, предполагая возможные рассуждения Пьера Ферма в отношении знаменитого уравнения в основе своей аналогичными приведенным выше.

Давайте теперь воображать дальше. Осознав связь производной функции с самой функцией, дальше Пьер Ферма в принципе мог приблизиться к пониманию приращения функции как составной величины: суммы какой-то главной части приращения, пропорциональной приращению независимой переменной, и некоторой бесконечной малой величины, вносящей лишь побочный вклад в общее приращение. Эту главную часть приращения сегодня называют дифференциалом и обозначают перед именем переменной символом d или же знаком ∂ для частных дифференциалов (в то время как приращение обозначают знаком "дельта": Δ). Соответственно есть дифференциал аргумента функции: dx, и есть дифференциал значения функции (обычно просто говорят дифференциал функции): dy.

Дифференциал функции, записью которого является dy=ƒ'(x)dx, в общем-то можно понимать как предполагаемое приращение зависимой переменной y на участке dx приращения независимой переменной x, ибо такое приращение не учитывает вклад в общее приращение той упомянутой бесконечно малой величины. Указанная запись означает следующее: дифференциал функции в точке x есть первая производная функции в точке x, умноженная на дифференциал аргумента. Читать ее можно и так: предполагаемое приращение значения функции на участке между точками x и x+dx вычисляется умножением имеющей место в точке x скорости изменения значения функции на длину dx участка. Ясно, что чем меньше длина участка, тем ориентировочно оцененная величина приращения ближе к действительному значению.

Вообще отличие дифференциала функции и ее приращения можно проиллюстрировать геометрическим образом: если на кривой линии графика функции y=ƒ(x) избрать точку с координатой x₁y₁ и провести касательную к кривой в этой точке, а затем на кривой избрать отстоящую далее точку с координатой x₂y₂, то приращение функции будет равно приросту координаты y кривой графика во второй точке (то есть Δy=y₂-y₁), в то время как дифференциал функции будет равен приросту координаты y касательной (то есть dy=ƒ'(x)Δx=ƒ'(x)dx, где dx=Δx=x₂-x₁).

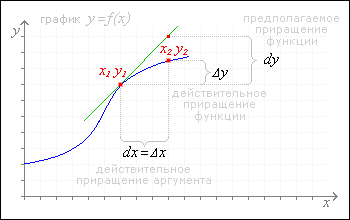
Еще один момент заключен в следующем: если между дифференциалом функции и ее приращением проводят различие, то между дифференциалом аргумента функции и приращением аргумента такого различия не делают, подразумевая аргумент x заданным линейной функцией вида x=ƒ(u)=u. На воображаемом графике этой линейной функции любому приращению аргумента u будет соответствовать такое же приращение значения x функции. Вот почему устанавливается равенство dx=Δx, которое означает: предполагаемое приращение аргумента функции всегда равно действительному приращению аргумента.

Заметка на всякий случай: В учении любой науке, когда встает необходимость овладеть какими-то ее нелегкими приемами или постичь непривычные представления, одним из стимулирующих факторов являются четкие примеры того, что это действительно кому-то нужно, что это полезно с практической точки зрения, что это можно задействовать не просто в воображении, но и в реальном деле. Приведем хотя бы один примитивный из таких примеров. Исполнитель спел песню; магнитофонную запись этой песни оцифровали, то есть перевели в цифровой формат, замеряя десятки тысяч раз в каждую секунду мгновенные показания амплитуды колеблющегося электрического сигнала на звуковом выходе магнитофона и сохраняя каждое показание в виде числа в памяти компьютера. Но ведь получается неимоверно длиннющий ряд чисел, притом каждое такое число в свою очередь представлено в двоичном виде с помощью какого-то фиксированного количества информационных единиц (битов). Можно ли без потери информации сократить количество битов? Может, какие-нибудь биты в той предлиннющей цепочке чисел вовсе лишние? Сегодня изобретено много способов, однако одним из первых, и к тому же достаточно эффективным (примерно 25 процентов "лишних" битов удаляется абсолютно без потерь исходной информации), был способ именно на базе представлений о приращении функции: вместо самих показаний амплитуды сохраняются приращения электрического сигнала с момента предыдущего показания амплитуды, вследствие чего количество чисел остается прежним, зато большинство чисел теперь оказываются меньшими, то есть достоверно записать их можно уже меньшим количеством битов. Вот какое полезное применение.

Так вот вообразим далее, будто Пьеру Ферма пришла в голову мысль выразить обе части уравнения ƒ(x_a)+ƒ(x_b)=ƒ(x_c) посредством дифференциалов: ƒ'(x_a)dx_a+ƒ'(x_b)dx_b=ƒ'(x_c)dx_c.

Очень хорошо суть идеи выражения уравнения посредством дифференциалов демонстрируется следующими геометрическими соображениями. Пусть выбрана некоторая степень n>1 для aⁿ+bⁿ=cⁿ, предположительно имеющего решения в натуральных числах. Каждый член равенства являет собой функцию вида y=xⁿ. Поэтому можно построить всего один график этой функции и на кривой линии графика обозначить сразу три такие точки (на рисунке они красного цвета), координаты x которых равны воображаемому целочисленному решению (x_a)ⁿ+(x_b)ⁿ=(x_c)ⁿ. Далее к кривой линии графика в этих трех обозначенных точках провести касательные (они изображены зеленым цветом). И тогда на этих касательных обязательно должны найтись смещенные на Δx относительно точек касания точки (они изображены черным цветом), в которых дифференциалы функции (то есть ее предполагаемые приращения) станут такими, что сумма первых двух из них будет равна третьему.

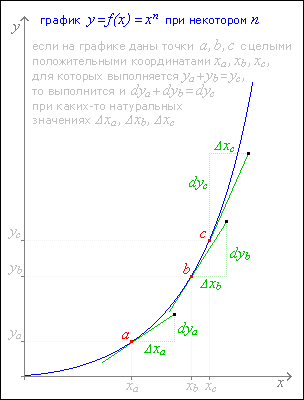
Но если дифференциал функции есть умножение производной функции на dx=Δx, возникает вопрос: чему равна производная функции y=ƒ(x)=xⁿ? Раз уж Пьер Ферма имел некоторое представление о производной, пусть и немного отличное от современного, он смог бы, наверное, подойти к заключению, что производной упомянутой функции оказывается функция y'=ƒ'(x)=nx^n-1 (напомним краткий путь к этому результату: берем выражение ((x+Δx)ⁿ-xⁿ)/Δx, раскрываем скобки, производим необходимые сокращения, полагаем Δx стремящимся к нулю, вследствие чего отбрасываем все члены, в которые Δx входит множителем; оставшиеся члены являются выражением производной ƒ'(x)).

В таком случае имеется равенство n(x_a)^n-1dx_a+n(x_b)^n-1dx_b=n(x_c)^n-1dx_c, и значит должны существовать какие-то натуральные dx_a, dx_b и dx_c, сохраняющие истинным записанное равенство. Но каковы они?

Сразу напрашиваются мало о чем говорящие тривиальные значения: dx_a=x_a, dx_b=x_b, dx_c=x_c. Тогда естественным образом получаем первоначальное уравнение с общим множителем n. Однако существуют и другие, более информативные значения: dx_a=(x_c)^n-1-x_a, dx_b=(x_c)^n-1-x_b, dx_c=(x_a)^n-1+(x_b)^n-1-x_c. Здесь можно еще раз вспомнить указанный много выше тот любопытный результат, когда из a^p+b^p=c^p через (c-q)^p+(c-s)^p=c^p выходим на q^p+s^p=cn. С последними указанными значениями дифференциалов равенство сохраняет силу: (dx_a)ⁿ+(dx_b)ⁿ=x_cm, то есть сумма их n-ых степеней делится нацело на x_c.

Теорема о дифференциальном составе степени двучлена

Разумеется, мы только допускали, что размышления Пьера Ферма могли развиваться в подобном направлении. Здесь интереснее другая деталь: из данных соображений нетрудно извлечь полезное дополнение к рассматривавшейся еще ранее теме бинома Ньютона, а именно сформулировать красивую теорему о дифференциальном составе степени двучлена, которая демонстрирует члены формулы бинома Ньютона в ином, непривычном ракурсе.

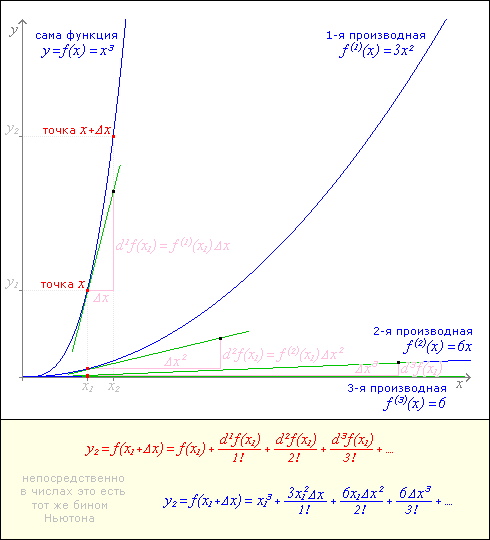
Теорема: значение функции y=ƒ(x)=xⁿ в точке x+Δx есть сумма значений в точке x самой функции и ее дифференциалов всех порядков (вплоть до n-ного) при dx=Δx, деленных каждый на факториал своего порядка.

То есть, если для обозначения порядка дифференциала привлечь символ r=1, то по содержанию теоремы имеется такое равенство: ƒ(x+Δx)=(x+Δx)ⁿ=ƒ(x)+d^rƒ(x)/r!+d^r+1ƒ(x)/(r+1)!+...+d^r+nƒ(x)/(r+n)! или в другом виде: ƒ(x+Δx)=(x+Δx)ⁿ=ƒ(x)+ƒ^(r)(x)dx^r/r!+ƒ^(r+1)(x)dx^r+1/(r+1)!+...+ƒ^(r+n)(x)dx^r+n/(r+n)!.

Полное доказательство теоремы приводить здесь уже не станем, так как оно в общем опирается на тот факт, что r-ный по счету (начиная счет с нуля) коэффициент C при члене разложения по формуле бинома Ньютона для показателя степени n вычисляется по формуле C_r=n!/(r!(n-r)!), а коэффициент у производной r-ного порядка от функции xⁿ - по формуле n(n-1)(n-2)...(n-r+1), что равно n!/(n-r)!. Но ведь при делении последнего выражения на факториал порядка производной, то есть на r!, мы как раз и получим коэффициент r-ного члена биномиального разложения.

Напоследок ради провокации воображения укажем расширенную, но немного некорректную формулировку теоремы: значение функции y=ƒ(x)=xⁿ в точке x+Δx есть сумма ее дифференциалов абсолютно всех порядков (от нулевого до бесконечности) в точке x при dx=Δx, деленных каждый на факториал своего порядка. Некорректность заключена в термине "дифференциал нулевого порядка"; он недействителен. Есть производная нулевого порядка, это сама исходная функция. Дифференциал нулевого порядка при dx=1 (так как dx⁰=1 при любом dx) - в принципе это тоже исходная функция, просто в силу определения дифференциала (что это все же основная часть относительного изменения переменной) такое понимание его некорректно. Что касается бесконечности порядков дифференциалов, а не сказанного ранее "вплоть до n-ного", то здесь все верно. Дифференциалы рассматриваемой функции порядков выше n-ного всегда нулевые, что можно строго доказать. Это демонстрируется и на рисунке: условно изображен график функции y=x³, графики ее производных вплоть до 3-го порядка еще не лежат на оси x, а вот графики производных остальных порядков уже лежат на этой оси. Из сказанного ясно, почему достаточно ограничиться суммированием дифференциалов только порядков вплоть до n-ного.

Дмитрий Сахань, 27 ноября 2006 года