Разделы
Счетчики
Задача: доказать, что хроматическое число 3-мерного пространства равно бесконечности
Шпаргалки для юных математиков
Пусть имеется следующая теорема: для трехмерного евклидова пространства существует схема расположения в нем соприкасающихся поверхностью объектов ненулевого объема, при которой потребуется бесконечно много цветов для такого отличительного окрашивания, чтобы никакие два соприкасающиеся объекта не были окрашены одинаковым цветом. Или то же утверждение в иной форме: хроматическое число трехмерного пространства равно бесконечности.
Вот такую чисто теоретическую задачу мне потребовалось решить, мое доказательство состоит из нижеследующих геометрических соображений, где в пунктах 1-3 изложено подготовительное построение, в последнем пункте дается логический вывод.
1) Произвольно выделим в пространстве плоскость и для удобства построений свяжем с ней двумерную систему координат XY. Пусть также существует Г-образного вида стержень, перпендикулярные друг другу части которого (условно назовем их "рукава") для простоты считаем бесконечно длинными. Пусть в нашем распоряжении имеется сколь угодно много таких Г-образных объектов.
2) Располагаем первый Г-образный объект поверх выделенной в пространстве плоскости так, чтобы угол объекта оказался в какой-нибудь произвольной координате x0, y0 и чтобы один его рукав был ориентирован вдоль оси y и, соответственно, другой рукав - вдоль оси x. Аналогично располагаем второй Г-образный объект поверх первого объекта, только смещаем второй объект по координатной сетке на некоторое расстояние Δx и Δy, то есть чтобы его угол оказался в координате x0+Δx, y0+Δy. Поверх этих объектов аналогично располагаем третий Г-образный объект в координате x0+2Δx, y0+2Δy. Над ними - четвертый объект в координате x0+3Δx, y0+3Δy. И так далее до бесконечности. То есть всякий указанный i-тый объект расположен над выделенной плоскостью в ее координате x0+(i-1)Δx, y0+(i-1)Δy.
3) Теперь "придавливаем" всю конструкцию к выделенной плоскости, чтобы деформация рукавов Г-образных объектов состояла только в огибании препятствий в лице пролегающих под ними рукавов других Г-образных объектов. В итоге конструкция примет подобный вид "плетения", как изображено на прилагаемом рисунке (на нем продемонстрировано только 7 объектов после "придавливания").
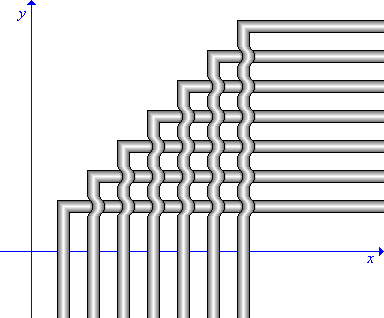
4) Сколько бы бесконечно много Г-образных объектов ни использовалось в указанной схеме расположения их в трехмерном пространстве, для всякого объекта окажется справедливым утверждение, что он одновременно соприкасается с остальными объектами, и следовательно его цвет при выполнении задания отличительного окрашивания должен быть не таким, как цвет остальных объектов. Утверждение можно сформулировать иначе: цвет i-того по счету объекта отличается от цветов, использованных для окраски объектов от первого по счету до i-1 включительно. Но тогда в силу этого утверждения, если начать окрашивание с первого объекта, обозначив номер текущего окрашиваемого объекта индексом i, на каждом следующем i-том шаге придется использовать i-тый по счету цвет. А значит хроматическое число здесь будет равно тому количеству объектов, которое было расположено в пространстве.
Вывод: поскольку наглядно продемонстрирована одна из возможных схем расположения в трехмерном евклидовом пространстве бесконечного множества неких объемных предметов (возможны и другие варианты объектов, не только Г-образные), каждый соприкасающихся одновременно с остальными объектами, то хроматическое число трехмерного пространства действительно равно бесконечности. Отсюда также следует, что хроматические числа пространств большей размерности не могут быть равными конечному числу, потому что всякое n-мерное пространство при n>3 уже включает в себя координатные плоскости системы координат трехмерного пространства.
Дмитрий Сахань, 18 марта 2007 года