Такие обворожительные простые числа

Простые числа - одно из чудес математики, загадка с более чем 2000-летней историей, столп современных систем криптографии. Многие вопросы, связанные с этими числами, не решены до сих пор и имеют не только философское, но и практичное значение. Уже хотя бы потому, что в наш век методы криптографии эффективно используют отсутствие стройной теории, способной ответить на любой вопрос касаемо простых чисел, особенно систематизировать их распределение в ряду чисел. Последнее вообще есть палка о двух концах. Теоретически такую задачу не представляется возможным решить безупречно, тем более что ее решение привело бы к краху многих методов шифрования, основанных на нынешней невозможности предсказать, чему равно, скажем, миллиард первое простое число, кроме как тривиальным пересчетом всех чисел в поисках указанного простого числа.

По тематике простых чисел существует немало материалов, профессиональных исследований. Назначаются впечатляющие премии за обнаружение неизвестных еще чисел Мерсенна (простые числа вида 2^X-1, где X - тоже простое число). Математический институт Клея учредил премию в 1 миллион долларов тому, кто убедительно докажет или опровергнет гипотезу Римана, связанную с распределением простых чисел в ряду натуральных чисел.

Заинтересованный и знающий человек может броситься в омут творческого поиска. Но несведущий рискует увязнуть в топях математических тонкостей. Как раз поэтому предлагаемый материал не ставит претенциозных целей что-либо доказать или опровергнуть. Цель банальнее некуда: легким слогом объяснить всякому, испытывающему сложности с математическими деталями, излагаемыми в профессиональных работах, некоторые важные моменты в природе простых чисел. Быть может, так человеку станет проще осознать план дальнейших шагов, прежде чем ринуться в собственные исследования.

Для освежения памяти

Вспомним сжато необходимые первоначальные сведения. Положительные числа 1, 2, 3 ..., появившиеся в результате счета, называются натуральными. Натуральных чисел бесконечно много. Наибольшее натуральное число назвать в принципе невозможно, поскольку бесконечность ряда таких чисел подразумевает обязательное наличие числа, больше любого названного на 1. В этих условиях правый край ряда натуральных чисел принято обозначать символом бесконечности (значок ¥).

Кроме того, всякое натуральное число относится либо к классу простых чисел, либо к классу составных чисел; соответственно, ряд натуральных чисел состоит из простых и составных чисел. Простое число делится без остатка только на само себя и на 1, отчего имеет лишь два положительных делителя. Когда натуральное число делится без остатка еще на какое-нибудь натуральное число, кроме самого себя и 1, такое число называется составным. Основная теорема арифметики гласит: каждое составное число может быть представлено в виде произведения простых чисел и притом единственным образом.

7 - простое число; делится без остатка только на 7 и 1
11 - простое число; делится без остатка только на 11 и 1

6 - составное число; делится без остатка на 6, 3, 2 и 1
9 - составное число; делится без остатка на 9, 3 и 1
15 - составное число; делится без остатка на 15, 5, 3 и 1

Дополнительно по натуральным числам можно сказать следующее. Единица условно считается простым числом, хотя она все же не является ни простым, ни составным числом, ведь единица имеет лишь один положительный делитель. Просто получается так, что единица удовлетворяет критерию простых чисел, ибо делится на саму себя и на 1, хотя делитель на самом деле получается один и тот же. Двойка - тот единичный случай, когда в класс простых чисел попало четное число. Вообще же среди простых чисел больше нет ни одного четного числа, поскольку другие четные числа больше 2 делятся как минимум на 2.

Простых чисел в ряду натуральных чисел тоже бесчисленное множество в том смысле, что простые числа продолжают появляться на всем протяжении ряда натуральных чисел, а не прерываются в какой-то точке ряда. Это следует из основной теоремы арифметики. Если бы появление простых чисел после некоторой точки ряда прекратилось, в ряду чисел непременно оказались бы числа-"дырки", которые уже невозможно представить произведением имеющихся простых чисел.

Вот простой пример. Пусть после 3 простые числа перестают появляться. Нам доступно всего три простых числа: 1, 2 и 3. Их произведениями можно представить следующие числа в числовом ряду. Легко показать таким образом число 4=2·2. Но как быть с числом 5? Появляется "дырка".

В одном случае, аксиоматизируя конечность простых чисел, мы вынуждены признать в нашем примере на числе 4 конечность ряда натуральных чисел, потому что такой ряд должен состоять из простых и составных чисел. Но в виду принятых нами ограничений число 5 нельзя признать простым (простые числа закончились на 3) и в то же время оно не попадает в класс составных чисел. А значит после числа 4 имеем уже не ряд натуральных чисел.

В другом случае, признавая бесконечность появления простых чисел, мы вынуждены признать бесконечность ряда натуральных чисел, поскольку каждое новое число-"дырка", не отражаемое произведением имеющихся простых чисел, признается новым простым числом, что в свое очередь постоянно расширяет ряд натуральных чисел в сторону бесконечности. Как следствие, то мнимое число, обозначаемое значком бесконечности, является простым числом.

Причины распределения простых чисел в ряду чисел

На секунду отвлечемся на такую тему как суть преобразования Фурье. Сложное периодическое колебание величины X можно представить в виде ряда Фурье, состоящего из простых гармонических колебаний с циклическими частотами, кратными основной циклической частоте w. То есть ряд Фурье состоит из гармоник с частотами: 1w, 2w, 3w, 4w и так далее. Фактически преобразование Фурье раскладывает сложное колебание в цепочку коэффициентов, каждый из которых формально указывает амплитудную характеристику соответствующей гармоники. Суть преобразования как раз в том и заключается, что вместо сложного колебания, кажущегося на первый взгляд не имеющим системной логики, мы получаем иную картину, откуда в полной мере видно, что сложное колебание на самом деле есть сумма таких-то гармоник. Сложив эти простые гармонические колебания вместе (обратное преобразование Фурье), получим в точном виде исходное сложное колебание.

Появление простых чисел в ряду натуральных чисел также видится беспорядочным. Однако здесь существует своя логика, требуется лишь взглянуть на простые числа по-иному. Например, разделив числа ряда на 2, замечаем, что каждое нечетное число не делится без остатка, а четные - делятся. Получается, четные числа подчиняются некоторому "колебательному процессу" с циклической частотой 2w. Пусть w для удобства примем равным 1 из соображений, что соседние числа ряда отличаются ровно на 1, поэтому дальше просто будем говорить о циклических частотах 2, 3, 4, 5 и так далее. А теперь изобразим упомянутый колебательный процесс при помощи синусоиды в ряду натуральных чисел, допустим, от 1 до 60.

На рисунке видно, что колебательный процесс погасил все четные числа после 2. Важно: и далее мы не будем гасить те числа, в которых синусоида колебательного процесса впервые входит в ряд натуральных чисел, если только в это число уже не входит другая синусоида. Как пример, мы не погасили число 2, и в это число не входит никакая другая синусоида (их еще попросту нет).

Давайте сюда введем следующую циклическую частоту, это 3. Но для наглядности слегка затеним синусоиду предыдущей частоты (чтобы не мешала), а синусоиду новой частоты сделаем чуть выше амплитудой. Итак, вводим еще один колебательный процесс.

Введенный процесс погасил еще некоторые непогашенные числа. Здесь хотелось бы обратить внимание на так называемые числа-"близнецы". Посмотрите: 5 и 7, 11 и 13, 17 и 19, и так далее. О "близнецах" обычно говорят, что это пары чисел, "волею случая" (поскольку система их появления считается загадкой) оставшиеся стоять в ряду чисел бок о бок со своим числом-"собратом". Мы можем сказать о "близнецах" пространнее.

Во-первых, "рождение" пар чисел непосредственно обязано колебательным процессам с частотами 2 и 3. Остальные колебательные процессы всего лишь вносят коррективы в расстояния между "близнецами" в правой части числового ряда, уничтожая одно из чисел-"собратьев", а то и всю пару целиком. Вообще скученность или разреженность простых чисел в правой части ряда обязана совместному действию колебательных процессов с нечетными частотами более 3.

Во-вторых, для "близнецов" выполняется следующее правило: их сумма кратна 3, причем остаток от деления (можно применить оператор mod) на 3 левого "собрата" должен быть равен 2, а правого "собрата" - 1. Именно по этим причинам "близнецами" считается пара 5 и 7, но никак не 3 и 5 (3+5=8, что не делится на 3 без остатка). Пусть для примера нам дали проверить пару 39 и 41 на принадлежность к "близнецам". Ответом будет "Нет", поскольку 39+41=80, и результат не делится на 3 без остатка. И совсем другой ответ будет на пару 41 и 43: 41+43=84, 84/3=28, (41 mod 3)=2, (43 mod 3)=1. То есть все условия соблюдены, и пара эта принадлежит "близнецам". А вот станет ли пара потенциальными "близнецами", зависит от действия колебательных процессов с нечетными частотами более 3.

Но вернемся к нашему ряду чисел и введем в него следующий колебательный процесс с частотой 4.

Заметьте, что процесс с частотой 4 прошелся по всем погашенным числам, так как этот процесс сам по себе кратен процессу с частотой 2. Идем дальше, вводим следующий процесс.

Обратите внимание на тот факт, что каждый новый колебательный процесс с нечетной частотой приводит к разрушению некоторых чисел-"близнецов". Например, последний процесс погасил "собратьев" у пар 23 и 25, 35 и 37, 53 и 55. Следующий колебательный процесс с частотой 7, к которому мы перейдем сразу, пропуская процесс с частотой 6 (ведь он из-за кратности процессу с частотой 3 пройдет по погашенным числам), тоже погасит часть "собратьев", например у пары 47 и 49.

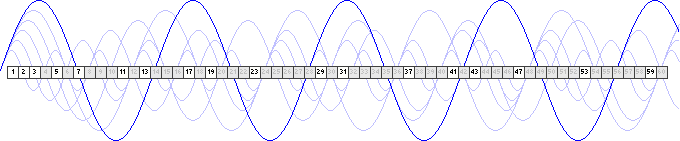
И вводить колебательные процессы так можно до конца ряда чисел, вплоть до бесконечности. Характерна здесь такая деталь: синусоиды тех процессов, что впервые входят в ряд чисел, показывают простое число, если к этому моменту такое число не было погашено синусоидами предыдущих процессов. Иначе говоря, если число X не принадлежит синусоидам колебательных процессов с частотами меньше числа X, тогда число X простое. Например, из следующего рисунка видно, что 19 - число простое, поскольку оно не принадлежит синусоидам процессов с частотами от 2 до 18, то есть ни одна из тех синусоид не пересекла число 19. То же будет и для чисел 23, 29, 31 и так далее.

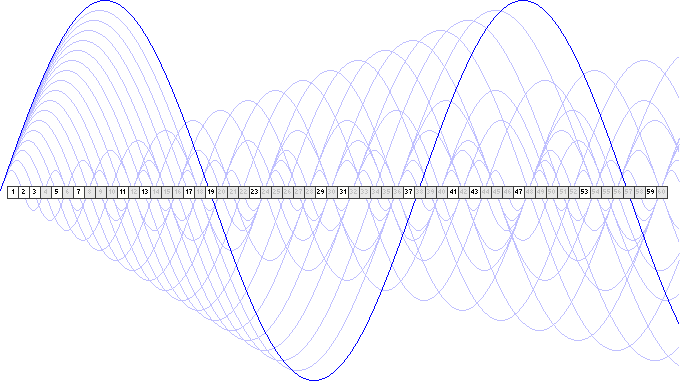
Посмотрим на оставшиеся непогашенные числа. Проводя аналогию с обратным преобразованием Фурье, весь ряд натуральных чисел с погашенными (составными) и непогашенными (простыми) числами - это сложное колебание, полученное из множества простых колебаний с циклическими частотами, равными числам натурального ряда. Однако если в преобразовании Фурье сложное колебание образуется суммой гармоник, то здесь сложное колебание образовано произведением гармоник.

Алгоритмическое определение простого числа

Из сказанного выше можно записать тригонометрическую форму условия принадлежности некоторого числа X классу простых чисел.

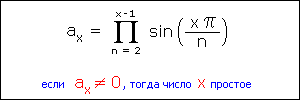
На всякий случай уточнения: здесь X обозначает анализируемое число, а n - конкретную циклическую частоту. Соответственно, n в цикле изменяется в пределах от 2 до X-1 включительно. Значок P говорит нам о том, что вычисляется произведение синусоид (за значком стоит функция синуса) всех частот n=2..X-1. Так вот если результирующий коэффициент a_x оказывается не равным нулю (или же, как говорят математики, произведение перечисленных элементов сходится), тогда число X не принадлежит ни одной из синусоид, следовательно, оно является простым.

Механизм действия формулы незамысловат. Синус аргументов Пи, 2Пи, 3Пи, 4Пи и тому подобных целых коэффициентов при числе Пи результатом всегда дает 0. Вместо коэффициента при числе Пи в формуле подставлено выражение X/n, и это значит, что как только некоторая циклическая частота n целиком (или же, по-другому, половинка синусоиды) укладывается один или более раз в диапазон чисел от 1 до X, то при числе Пи получаем целый коэффициент, что немедленно ведет к появлению в произведении числа 0. Как известно, умножение на 0 равно 0, сколько бы еще сомножителей ни стояло в выражении. Для простых чисел 0 в произведении ни разу не попадется. Вот в этом и заключен принцип работы формулы.

Впрочем, можно записать упомянутое условие принадлежности в арифметической форме. Вместо функции синуса ставим деление по модулю (оператор mod), и получаем произведение остатков от деления числа X на все циклические частоты n. Результат тот же самый.

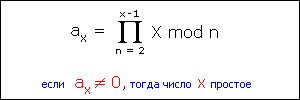
Изучение представленных формул дает нам основание заявить, что их применение для определения условия принадлежности для очень больших чисел потребует высоких вычислительных ресурсов. В самом деле, по последней формуле для чисел свыше миллиона необходимо вычислить не менее миллиона операций умножения (n=2..X-1, при X свыше миллиона), не считая такого же количества операций деления по модулю. Почти X² операций - это колоссальное количество, особенно при больших значениях X.

Однако не все так плохо. Можно значительно сократить количество операций, если прибегнуть к правилу: для любого составного числа X наименьший целый делитель, кроме 1, расположен в пределах от 2 до корень квадратный из X. Добавим сюда тот факт, что после 2 можем искать делитель только среди нечетных чисел (исключая четные числа 4, 6, 8 и так далее) вплоть до корень из X, а это сокращает диапазон еще в 2 раза. В итоге формулы приобретают алгоритмически лаконичный вид.

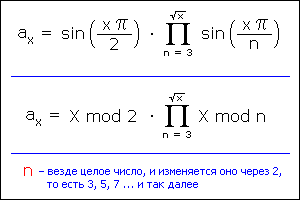
Здесь элемент колебательного процесса с четной частотой 2 вынесен из-под знака цепочки произведений, остальные элементы с нечетными частотами от 3 до корень из X оставлены под знаком. Получили минимум операций. Кстати, на сегодня это самый быстрый из доступных обывателю способов определения принадлежности числа X классу простых чисел, и причем это способ, справедливый на всем протяжении ряда натуральных чисел. Правда, данный способ все-таки не исключает долю лишних выполняемых действий. Так, например, после n=7 выполняется лишнее n=9, и лишнее оно потому, что уже было выполнено кратное ему n=3. Фактически среди нечетных чисел n=3..корень из X встречается достаточно составных чисел, которые сами по себе лишние в вычислениях. Алгоритмически выгодно избежать этого пока не удается. Действие по избежанию лишних вычислений иногда оказывается затратнее, чем выполнить само лишнее вычисление.

Напоследок приводится алгоритм, воспроизведенный по последней формуле с делением по модулю. Входным параметром функции является любое целое положительное число от 1 до бесконечности. Если входной параметр содержит простое число, тогда функция возвратит значение ЭТО_ПРОСТОЕ_ЧИСЛО. Иначе будет возвращено значение ЭТО_СОСТАВНОЕ_ЧИСЛО. В теле функции используется оператор деления по модулю - mod, то есть разделить и взять только остаток от деления. Четные числа анализируются прямо в начале функции. Все они, естественно, не дают остатка (НЕТ_ОСТАТКА) при делении на 2, однако только двойка при делении на 2 дает частное 1. Именно последний признак позволяет в теле функции отнести все четные числа, кроме 2, к классу составных.

функция КакоеЭтоЧисло( Искомое_Число ): Результат

  объявляем локальную переменную Предел
  объявляем локальную переменную Делитель

  Результат = ЭТО_СОСТАВНОЕ_ЧИСЛО

  если Искомое_Число mod 2 = НЕТ_ОСТАТКА тогда
    если Искомое_Число / 2 <> 1 тогда выйти
  конец если

  Предел = корень квадратный из Искомое_Число
  Делитель = 3

  цикл пока Делитель <= Предел
    если Искомое_Число mod Делитель = НЕТ_ОСТАТКА тогда выйти
    Делитель = Делитель + 2
  конец цикла

  Результат = ЭТО_ПРОСТОЕ_ЧИСЛО
конец функции

Рекомендуется дополнительно прочитать продолжение темы простых и составных чисел, где рассматриваются генераторы таких чисел.

Дмитрий Сахань, 30 ноября 2004 года