Разделы
Счетчики
О секретах простых и составных чисел
Тысячи лет натикали часы с того мгновения, когда человек впервые употребил знаковые обозначения для количества исчисляемых предметов. Этими символами были цифры. Соединяя изобретенные знаки по придуманным ним самим же правилам, человек сотворил основное понятие математики - число, тем самым пробудив к жизни неслыханные дотоле законы отношений между числами. Изучение неведомых законов происходило долго и мучительно и дало человеку многое, а некоторые потаенные связи, так и оставшиеся непознанными с тех незапамятных времен, продолжают терзать математиков и сегодня. К числу таких, на внешность кажущихся посильными к осмыслению, относятся тайны простых и составных чисел.
Что такое простое число? Это натуральное (целое положительное) число p, которое невозможно разделить нацело на любое другое натуральное число, отличное от единицы и самого числа p. Обычно говорят, что всякое простое число делится нацело только на само себя и на единицу, а в популярной литературе такое число нередко обозначают первой буквой словосочетания "prime number - простое число". Примеры малых простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 и так далее. Между простыми числами в ряду натуральных чисел находятся составные числа, получившие свое название из того наблюдения, что все они составлены произведением каких-нибудь простых чисел. Соответственно, составных чисел намного больше, чем простых. Например, все четные числа, кроме 2, относятся к составным, так как образованы умножением натурального числа n>1 хотя бы на одну двойку. А это уже половина ряда чисел. Добавим сюда и те нечетные числа, образованные всевозможными комбинациями произведения простых множителей. В общем, очень много составных чисел.
Математиков давно волновал вопрос: сколько простых чисел находится в ряду натуральных чисел перед произвольно заданным числом n? Точная формула для вычисления этого количества - его обозначают p(n) - не найдена до сих пор. Со второй половины 19 века существует только приблизительное выражение p(n)»n/ln n, которое отражает асимптотический закон распределения простых чисел (асимптотический - всего лишь приближенный к точному).
В отношении простых чисел интересовали математиков также вопросы отнюдь не праздные. Среди важных стояла проблема: существует ли такое выражение, следуя которому можно было бы вычислить любое простое число по желанию? С ее решением пришло бы широкое понимание многих вещей в теории чисел, а отсюда могли родиться новейшие исследовательские методы и практические приложения в сопряженных областях науки. Особо красивым виделось обнаружение функциональной зависимости f(i)=p, в которой аргумент i был бы порядковым номером по счету для простого числа p, так сказать, его индексом. Скажем, простое число 17 расположено седьмым по счету после простых чисел 2, 3, 5, 7, 11 и 13. Так вот хороша была бы функция, где f(7)=17, f(8)=19, f(9)=23, f(10)=29 и так далее. Но сама зависимость и по сей день остается тайной за семью печатями.
Ее поиски с давних времен происходили больше наугад, ведь по-иному нельзя действовать в условиях крайне ограниченных представлений о природе простых чисел. Сначала все начиналось с выражений вида 2k±1, 4k±1, 6k±1 и тому подобных. Такие выражения приводят к интересовавшим математиков нечетным числам, ведь все четные числа (в арифметике четность натурального числа принято выражать записью 2n), за исключением 2, и так относятся к составным. Но беда этих выражений заключалась в том, что они лишены качеств предсказуемости результата: подставляя очередное натуральное число k, мы не имеем ни малейшего шанса предвидеть, каким получится итог - простым или составным числом. Числа следуют вперемешку, к тому же чем выше множитель при k, тем больше происходит пропусков чисел, то есть следующее генерируемое число вовсе не представляется подлинно следующим числом в ряду чисел.
История хранит также выражение 2p-1, где показатель степени p равен простому числу. Французский монах Марен Мерсенн в начале 17 века занимался совершенными числами (так называется число, сумма делителей которого, кроме наибольшего, равна самому числу; например, 1+2+3=6). Числа вида 2p-1 упоминал еще Евклид в 3 веке до нашей эры, сообщая, что четные совершенные числа могут быть получены как 2p-1(2p-1), если число 2p-1 равно простому. Благодаря увлечению Мерсенна совершенными числами выражение 2p-1 понемногу предстало в образе темы простых чисел, а полученные по нему простые числа стали со временем называть числами Мерсенна. Вообще, по строгости, числами Мерсенна называется любое число вида 2p-1, будь оно хоть простым, хоть составным. А поскольку интерес представляли простые числа, то выражение "простые числа Мерсенна" просто сократили до "числа Мерсенна", обязательно подразумевая, что упоминаются исключительно простые числа. Однако таких простых чисел к сегодняшнему дню найдено всего несколько десятков и поиск каждого следующего обеспечивается длительным процессом последовательного перебора, так что претендовать на роль стабильного генератора данное выражение, безусловно, не могло.
На заметку: поиск чрезвычайно больших простых чисел Мерсенна ныне имеет и материальную подоплеку. Наибольшее известное в наше время число состоит из более чем 6 миллионов цифр. Любой человек, кто сообщит простое число 2p-1 с не менее чем 10 миллионами знаков, может получить премию в размере 100 тысяч долларов США. Только задача эта не из легких: масса компьютеров годами перебирают все простые показатели степени p, прежде чем обнаружится следующее простое число 2p-1.
Вслед за Мерсенном возник Пьер Ферма со своей гипотезой f(i)=22^i+1=p, где число p предполагалось быть простым при любом натуральном значении аргумента i. Действительно, при первых пяти значениях i=0..4 получаются простые числа: 3, 5, 17, 257 и 65537. Позже выяснилось, что дальше выходят одни составные числа, так что формула Ферма с подавляющим превосходством давала скорее составные числа, чем являлась генератором простых. К тому же пропуски между числами были огромными, отчего и речи не могло быть о том, чтобы аргумент такой функции воспринимался как порядковый номер простого числа.
Была еще формула Леонарда Эйлера - f(i)=i2-i+41=p, которая генерировала подряд 40 простых чисел при i=1..40: вот они - 41, 43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601. Затем числа начинали генерироваться вперемешку с составными. Это был уже качественно лучший результат, но все же и ему были присущи прошлые трудности. Во-первых, не удалось избежать перемешивания чисел, что объяснимо следующим образом: генерация одних лишь простых чисел не может быть осуществлена на базе формулы с единственной переменной. Во-вторых, порядковая нумерация генерируемых простых чисел и в случае формулы Эйлера не соответствует их нумерации в ряду чисел и с продолжением все больше расходится. В-третьих, генерация осуществляется только от простого числа 41.
Однако именно продемонстрированный труд Эйлера в большей мере ликвидировал пессимизм не только в вопросах, реально ли человечеству даже "вслепую" отыскать полные или, быть может, отрывочно совпадающие функциональные зависимости, но и в такой принципиально значимой проблеме: сколь сложной окажется такая функция? Со временем было доказано, что подобная функция, если она существует, есть многочлен как минимум с двумя переменными, причем достижение этого минимума выглядело настоящей утопией. Возникли две позиции: одна склонялась к отсутствию предела в количестве переменных (по аналогии с отсутствием предела в количестве простых чисел, каждое из которых уникально), следовательно к недостижимым вычислительным запросам такого многочлена; другая, наоборот, предпочла возможность наличия теоретического минимума переменных, которые предположительно должны были быть рациональными. Впрочем, это не подвинуло дело, поскольку нелегко было постановить, с какого конца браться за работу при крайне слабо постигнутых законах распределения чисел.
Второй существенной деталью труда Эйлера стало косвенное подтверждение авантюрного предубеждения, что формулу генерации простых или же, наоборот, составных чисел потенциально предъявить как диофантову задачу, решаемую либо исключительно в целых числах, либо только в рациональных (частично в целых, частично в дробных, или только в дробных). Однако обратный путь у такой задачи, от известного сгенерированного числа к восстановлению значений переменных в гипотетическом многочлене, предполагается быть необычайно трудным.
После изложенного краткого экскурса в историю рождения генераторов простых чисел есть повод вернуться в современную эпоху и приобщиться к свежим изысканиям. Ранее мы изучали простые числа через понятие колебательных процессов. В новом материале поговорим о генераторах чисел и некоторых теоремах и определениях, хотя и в этот раз читатель не сможет получить идеальную формулу генератора простых чисел с безупречным базисом. Но кое-что стоящее внимания, так сказать, пища для размышлений найдется безусловно.
Генерация чисел
Начнем с генерации составных чисел. Обратно определению для простого числа, составное число c (по аналогии его обозначим первой буквой словосочетания "composite number - составное число") - это произведение двух или более отличных от единицы натуральных множителей. То есть в самом простом виде c=xy. С четными составными числами дело ясное (это формула f(i)=2i+2=c, где i - порядковый номер четного составного числа), интереснее как раз нечетные числа. Поэтому числа x и y сразу рассматриваем только как нечетные натуральные числа. В арифметике принято нечетность числа выражать записью 2n+1, и пусть так мы обозначим число x, а число y обозначим записью 2m+1.
В итоге приходим к такому выражению: c=xy=(2n+1)(2m+1)=2(2nm+n+m)+1. Весьма интересно, что это вариант формулы 2k+1 древних исследователей, только число k теперь приобрело зависимость 2nm+n+m. Ну а функция f(m,n)=2(2nm+n+m)+1=c генерирует только нечетные составные числа при натуральных аргументах m>0 и n>0. Нет ни одного простого числа, которое можно было бы получить этой функцией, и нет ни одного нечетного составного числа, которое нельзя было бы не получить этой функцией.
Нумерация генерируемых чисел здесь напоминает матричную. Скажем, для f(m,n) аргумент m указывает порядковый номер ряда (строки) составных чисел, включающих множитель 2m+1, аргумент n - порядковый номер второго множителя составного числа в пределах выбранной строки.
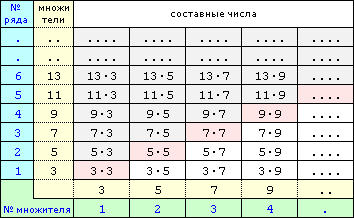
Правда, в такой нумерации не избежать дублирования чисел. То есть при матричной порядковой нумерации внутри условной матрицы обязательно существует линия, по бокам от которой находятся одинаковые ячейки. На рисунке эта линия выделена красноватым цветом, и сверху серым цветом помечены ячейки с такими же значениями, как у белых ячеек справа от линии. Так что невольно формула f(m,n)=2(2nm+n+m)+1=c заставляет дублировать составные числа. К тому же досконально подлинную нумерацию составных чисел, как они в действительности расположены в ряду натуральных чисел, так не получить. Здесь прослеживается четкое разделение по строкам с выделением конкретного множителя, и уже относительно этого множителя соблюдается истинное следование составных чисел. Но оно, еще раз уточним, не имеет общего со следованием составных чисел в ряду натуральных чисел, так как в этом ряду как бы произведено наложение всех строк матрицы в один ряд.
Устранить многие проблемы с дублями можно за счет мелкого видоизменения формулы. Продолжая считать аргумент m порядковым номером выбираемой строки, примем аргумент n в роли индекса генерируемого числа относительно разделяющей линии в матрице. Проще говоря, выбираем строку, а индексом указываем смещение необходимой ячейки вправо от помеченной красным цветом ячейки выбранной строки. Тогда языком математики такой выбор ячейки со значением составного числа c эквивалентен следующему выражению c=(2(m+n)+1)(2m+1)=(2m+2n+1)(2m+1), где m>0 и n³0. Отсюда приходим к c=4m2+4mn+4m+2n+1=2(2m2+2mn+2m+n)+1. Следовательно, видоизмененная функция f(m,n)=2(2m2+2mn+2m+n)+1=c - это тоже число вида 2k+1, просто число k приобретает зависимость 2m2+2mn+2m+n. Кроме того, и само число k есть число вида 2k’+a, так как k=2m2+2mn+2m+n=2(m2+mn+m)+n (это замечание - всего лишь любопытное наблюдение).
Еще одно занимательное наблюдение связано с тем, что в последних скобках оказалось выражение, родственное квадратному трехчлену (ax2+bx+c), только свободный член c здесь выходит равным переменной m. Ну и не тайна, что многие процессы физического характера подчиняются квадратичной зависимости. Простейшая квадратичная функция y=ax2 - это парабола, а функция y=ax2+bx+c - тоже парабола, только со смещенной вершиной на координатной оси. Отсюда выражение m2+mn+m - тоже парабола с начальной вершиной в точке (-n/2, -(n2-4m)/4). И поскольку свободный член оказывается переменной, ветви параболы "завалены" набок, а ее вершина постоянно смещается или, если выражаться терминами предыдущего материала, каждому числу соответствует свой колебательный процесс.
Но вернемся к генераторам чисел. Итак, функция f(m,n)=2(2m2+2mn+2m+n)+1=c, где аргумент m является порядковым номером выбираемого ряда (строки) составных чисел и аргумент n является индексом (смещением) от начала недублирующегося участка выбранной строки, генерирует нечетные составные числа только из правой части условной матрицы.
Однако абсолютно избавиться от дублей не получится, так как в правой части матрицы существуют дубли, обусловленные тем, что нумерация строк и индексация ячеек не учитывают попадание на строку или столбец с составным множителем. Например, f(4,3)=9·9=81 и f(1,12)=3·27=81. В принципе обыкновенное исключение всех строк с составными множителями начисто решило бы проблему. На словах это сделать легко, достаточно ввести условие: аргумент m сам не должен удовлетворять целочисленному равенству m=2n’m’+n’+m’ (это фрагмент формулы генерации нечетных составных чисел).
В общем, думается, читатель успел заметить, что генератор составных чисел являет собой настоящую диофантову задачу, решаемую в целых числах. Уравнение этой задачи может быть записано во множестве видов, от многочлена с двумя переменными до бесконечного их количества. Справедливо и следующее: такое уравнение можно представить и линейными, и квадратными, и прочими формами. Мы, к примеру, записали два самых простых вида: 2(2nm+n+m)+1=c и 2(2m2+2mn+2m+n)+1=c.
Без ложки дегтя, конечно, не обходится. Обратное решение задачи вообще неизвестно. Когда дано нечетное составное число c, поди-ка найди, какими значениями аргументов оно сгенерировано. Помогает незначительно то обстоятельство, что для любого составного числа наименьший отличный от единицы целочисленный делитель не больше [√c], где квадратные скобки означают "целая часть числа". Следовательно, аргумент m не может быть больше ([√c]-1)/2. Но для больших чисел этого явно мало, чтобы устранить необходимость перебора.
Генерация простых чисел. Качественная формула неизвестна. Пожалуй, она была бы одной из самых желаемых в мире математики, да к великому сожалению, тут путного сказать пока ничего не получается, разве что такая формула должна одновременно давать результаты, противоположные результатам формул f(i)=2i+2=c, f(m,n)=2(2nm+n+m)+1=c, f(m,n)=2(2m2+2mn+2m+n)+1=c и им подобным. Не исключено, что упор на решение приведенных уравнений в рациональных числах, например вида a/2, где a не должно быть четным (ибо тогда снова вернемся к прежнему уравнению в натуральных числах), имеет хоть сколько-нибудь оправданный резон, только без убедительных оснований такое смахивает на гадание на кофейной гуще.
Представимость разницей квадратов
Теорема о представимости простых чисел разницей квадратов: любое простое число большее 2 может быть представлено разницей квадратов двух натуральных чисел разной четности, притом единственным образом, и причем разница между этими натуральными числами всегда будет равняться 1.
Доказательство. Пусть p - какое-то простое число большее 2, m и n - натуральные числа разной четности, подчиняющиеся требованию m>n>0, а также требованию m-n=1. Из заявленной теоремы следует выполнение равенства p=m2-n2 лишь для единственных значений чисел m и n. Разложив разницу квадратов на произведение суммы и разницы натуральных чисел p=(m+n)(m-n), нам придется согласиться, что равенство имеет силу только в том случае, когда m-n=1 и m+n равно простому числу p, то есть когда равенство можно эквивалентно записать как p=(m+n)·1. Но если m и n различаются более чем на единицу, тогда в последнем равенстве вместо множителя 1 появляется больший множитель, и значит правая часть равенства не может быть простым числом, ведь она тогда состоит из произведения двух множителей больших 1 - а это уже составное число. Теорема доказана.
К слову сказать, отыскать единственные натуральные числа, подходящие для представления известного простого числа p>2 разницей квадратов двух этих чисел, совсем не сложно. Вот эти формулы: m=(p+1)/2, n=(p-1)/2. На самом деле они эквивалентны формулам m=((m+n)+(m-n))/2 и n=((m+n)-(m-n))/2, просто при задаче отыскивания чисел m и n нам известно как раз значение числа p, и мы к тому же точно знаем, что m+n=p и m-n=1. Именно эти выражения мы и подменили в формулах известным числом p и единицей. Например, нужно представить простое число 43 разницей квадратов двух натуральных чисел. Вычисляем m=(43+1)/2=22 и n=(43-1)/2=21. В результате получаем 43=222-212.
Теорема о представимости составных чисел разницей квадратов: любое нечетное составное число может быть представлено разницей квадратов двух целых неотрицательных чисел разной четности, притом не менее чем двумя способами.
Доказательство. Пусть c - какое-то нечетное составное число, m и n - целые неотрицательные (натуральные или нуль) числа разной четности, подчиняющиеся требованию m>n³0. Из сформулированной теоремы снова следует выполнение равенства c=m2-n2, которое опять разлагается к виду c=(m+n)(m-n). Как и для представления простых чисел, составное число также можно получить по пути m-n=1 и m+n равно составному числу c, из чего вытекает: m=(c+1)/2, n=(c-1)/2. Это первый способ, когда m-n=1.
В то же время m-n может равняться и какому-то другому отличному от единицы множителю составного числа c (обозначим этот множитель символом y), и тогда m+n - произведению остальных множителей этого числа (обозначим его символом x). То есть c=(m+n)(m-n)=xy. Предположим, что известны только x и y, тогда приходим к формулам m=(x+y)/2, n=(x-y)/2. Но поскольку y=m-n>1, значит это уже второй способ. Кроме того, y=m-n может быть равен и еще другому множителю составного числа c. Это будет третий способ. И так далее - четвертый способ, пятый, ... Теорема доказана.
Укажем примеры в числах: дано составное число 75, нужно представить его разницами квадратов двух натуральных чисел. Представим число 75 первым способом. Вычисляем m=(75+1)/2=38 и n=(75-1)/2=37. В результате получаем 75=382-372. Теперь представим число 75 другим образом, для чего разложим его в произведение простых множителей 75=3·5·5. Извлечем раздельно его множители y=3 и x=5·5. И далее вычисляем m=(5·5+3)/2=14 и n=(5·5-3)/2=11. В итоге имеем 75=142-112. Представим еще и третьим образом, для чего извлечем раздельно другие его множители y=5 и x=3·5. И затем вычисляем m=(3·5+5)/2=10 и n=(3·5-5)/2=5. В результате получаем 75=102-52.
Вот эти две теоремы тоже прекрасно дополняют точку зрения, согласно которой задача о простых или составных числах - это диофантова задача. И та и другая теоремы утверждают равенство для нечетного числа a=m2-n2. Если правая часть равенства решается в целых числах единственным образом, тогда левая часть непременно есть простое число. Иначе левая часть - составное число.
Да вот трудность в том, пожалуй, и заключается, что пока не видны очевидные шаги, по которым скорейшим образом можно было бы для известного числа a, не прибегая к разложению его в произведение простых множителей, найти второе представление числа a разницей квадратов двух натуральных чисел, подтвердив тем самым, что a - число составное. Без разложения в произведение множителей приходится действовать методом перебора чисел m и n. То же справедливо и в случае предположительно простого числа a, поскольку элементарно найдя m=(a+1)/2 и n=(a-1)/2, невозможно утверждать простоту числа a, не обнаружив отсутствие второго решения, что без разложения в произведение множителей приходится снова делать методом перебора.
Как генератор исключительно простых чисел, такая формула f(m,n)=m2-n2=p теоретически могла бы использоваться, если бы обнаружились фундаментальные отношения между натуральными числами m и n для всех простых чисел. Пока известно только m-n=1. Отсюда несложно записать формулу по-иному, без числа m: f(n)=(n+1)2-n2=2n+1=p. Но тут уже приходим к первичным формулам древних исследователей.
Зато в качестве генератора нечетных составных чисел формула f(m,n)=m2-n2=c более результативна, хотя не лишена недостатков, в частности неудобства соблюдения последовательности генерируемых чисел. Здесь только нужно помнить, что m-n>1 и, естественно, числа m и n - целые неотрицательные различной четности. Например, f(3,0)=32-02=9, f(4,1)=42-12=15, f(5,2)=52-22=21, f(5,0)=52-02=25, f(6,3)=62-32=27, f(7,4)=72-42=33, f(6,1)=62-12=35, f(8,5)=82-52=39, f(7,2)=72-22=45, f(7,0)=72-02=49 и так далее.
Определение для систем счисления
Следующая информация скорее всего станет полезной тем исследователям и практикам, кому приходится иметь дело с системами счисления.
Определение: десятичное натуральное число n является простым тогда и только тогда, когда в какой-нибудь p-ичной системе счисления (где p - простое число) число n записывается как 10p. Можно ввести несущественное дополнительное условие, которое лишь позволяет свести анализ числа к меньшему количеству действий. Вот это условие: причем не находится ни одной другой p-ичной системы счисления, в которой младший знак записанного в ней числа n равен нулю.
В самом деле, в любой системе счисления младший знак записанного числа всегда содержит результат деления исходного числа по модулю основания системы счисления. Действие деления по модулю обозначается оператором mod и по сути представляет собой получение неделящегося нацело остатка от деления одного числа на другое (эквивалентно такому выражению: a-[a/b]·b, где квадратные скобки означают "целая часть числа"). Как только в некоторой системе счисления младший знак записанного числа становится равным нулю, то значит число делится нацело на основание этой системы счисления. Простое число делится нацело на основание той p-ичной системы, которое равно этому числу, и оно в такой системе счисления будет записано непременно в форме 10p, в остальных p-ичных системах младший знак числа примет ненулевой остаток от деления.
Например, пусть нужно проанализировать десятичное число 7. Во время анализа основание системы счисления будет сменяться в соответствии с последовательностью простых чисел. То есть p=2, p=3, p=5, p=7 и так далее. Оценка последнего знака в числе производится на основе выражения 7 mod p=?.
Итак, анализируем число 7. В двоичной системе записывается как 1112 - младший знак 7 mod 2=1. В троичной системе - 213 - младший знак 7 mod 3=1. В пятеричной системе - 125 - младший знак 7 mod 5=2. В семеричной системе - 107 - младший знак 7 mod 7=0. В системах p>7 - 7p - младший знак 7 mod p=7.
Видно, что только в одной системе счисления число было записано в форме 10p и ни в одной другой системе младший знак не был равен нулю, следовательно анализировалось простое число.
Еще пример: десятичное число 9. В двоичной системе - 10012 - младший знак 9 mod 2=1. В троичной системе - 1003 - младший знак 9 mod 3=0. В пятеричной системе - 145 - младший знак 9 mod 5=4. В семеричной системе - 127 - младший знак 9 mod 7=2. В системах p>7 - 9p - младший знак 9 mod p=9.
Ни в одной системе число не было записано в форме 10p, следовательно это составное число. В этом примере введенное ранее дополнительное условие позволяло нам прервать анализ сразу после второго шага. Дело в том, что на втором шаге (в троичной системе счисления) обнаружен нуль в младшем знаке числа, но это число записано не в той форме. Если бы даже далее гипотетически обнаружилось число в форме 10p, то уже в двух системах имеются нулевые младшие числа.
Еще пример: десятичное число 15. В двоичной системе - 11112 - младший знак 15 mod 2=1. В троичной системе - 1203 - младший знак 15 mod 3=0. В пятеричной системе - 305 - младший знак 15 mod 5=0. В семеричной системе - 217 - младший знак 15 mod 7=1. В одиннадцатеричной системе - 1411 - младший знак 15 mod 11=4. В тринадцатеричной системе - 127 - младший знак 15 mod 13=2. В системах p>13 - "15"p - младший знак 15 mod p="15". Заметьте, двузначное десятичное число 15 взято в кавычки затем, чтобы напомнить, что это число является числом однознаковым в системе счисления с указанным основанием.
Ни в одной системе число не было записано в форме 10p, следовательно это составное число. И к тому же более чем в одной системе младший знак числа оказался равен нулю, то есть и здесь для анализа было достаточно двух шагов, применяя дополнительное условия.
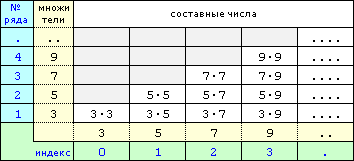
Вообще надо отметить, что записанные в p-ичных системах счисления числа представляют собой удобное средство выяснения, включает ли в себя исходное десятичное число множители, равные основанию системы счисления, и сколько именно таких множителей включает. Сколько нулей непрерывно следует в младших знаках p-ичного числа ap, столько же множителей p включает в себя исходное десятичное число n. Скажем, у двоичного числа 11101011000002 в младших знаках непрерывно следуют 5 нулей, и это значит, что десятичное число будет равно 2·2·2·2·2·x, где x - это произведение отличных от двоек простых чисел.
Исключительно по одним нулям в младших знаках p-ичных чисел можно восстановить исходное десятичное число, если в наше распоряжение предоставили все p-ичные числа, содержащие нули в младших знаках. Вот небольшой пример, где от нас будто бы намеренно закрыли символами точек все знаки до нулевых младших знаков, причем дали вообще все p-ичные числа. Допустим привели нам такие числа: ......2, ..003, ..05, "."p>5. В троичной системе счисления видим 2 нуля в младших знаках, в пятеричной - 1 нуль, из чего следует, что исходное число было таким: 3·3·5=45. Отсюда можно с точностью восстановить тот ряд чисел, который нам привели в закрытом виде: 1011012, 12003, 1405, "45"p>5.
Ну и на всякий случай напомним алгоритм перевода десятичного числа n в p-ичную систему счисления. Шаг 1: делим n по модулю на число p, то есть n mod p="?" (помните, что кавычками мы закрепляли однознаковую емкость результата в пределах p-ичной системы, даже если результат в десятичной системе занимает несколько знаков), и этот результат "?" каждый раз записываем в следующий старший знак (левее предыдущего результата). Шаг 2: делим n на число p и берем только целую часть итога, присваивая его вместо прежнего n, то есть выполняем следующее действие ni=[ni-1/p], где индекс i обозначает новое состояние числа n. Если новый n больше нуля, переходим снова к шагу 1, иначе останавливаемся.
Для примера переведем десятичное число 1046 в семнадцатеричную систему счисления.
Шаг 1: 1046 mod 17 = "9"
Преобразованное число = "9"17
шаг 2: [1046 / 17] = 61
Не равно нулю, значит снова шаг 1
Шаг 1: 61 mod 17 = "10"
Преобразованное число = "10"9"17
шаг 2: [61 / 17] = 3
Не равно нулю, значит снова шаг 1
Шаг 1: 3 mod 17 = "3"
Преобразованное число = "3"10"9"17
шаг 2: [3 / 17] = 0
Равно нулю, значит останавливаемсяЧтобы перевести 17-ричное число "3"10"9"17 обратно в десятичную систему счисления, нужно сложить все знаки числа, предварительно умножая каждый знак на основание исходной системы счисления, возведенное в степень, равную порядковому номеру знака, начиная нумерацию знаков с нуля от младшего знака к старшему. То есть 3·172+10·171+9·170=1046. Обычно последнее умножение с возведенным в нулевую степень числом опускают, поскольку там всегда получается умножение на единицу. Таким образом, 3·172+10·171+9=1046.
Из предоставленной информации вытекает не менее важное положение: десятичное число, записанное с нулевым младшим знаком в любой c-ичной системе счисления (где c - составное число), не может быть простым.
Дмитрий Сахань, 15 июня 2005 года